题目内容

若a∈R，且loga（2a+1）＜loga（3a）＜0，则a的取值范围是（　　）
A、（0，
1
3
）
B、（0，
1
2
）
C、（
1
2
，1）
D、（
1
3
，1）
考点：指、对数不等式的解法
专题：函数的性质及应用
分析：利用函数的单调性求解，2a+1＞0，3a＞0，分情况进行讨论．
解答： 解：∵2a+1＞0，3a＞0，
当a＞1时，2a+1＜3a＜1，
解得：a∈∅；
当0＜a＜1时，原不等式可转化为：2a+1＞3a＞1，
解得：
1
3
＜a＜1．
故选D．
点评：本题主要考查利用函数单调性定义解抽象不等式，一般来讲，抽象不等式的解法是利用函数的单调性．
练习册系列答案
相关题目
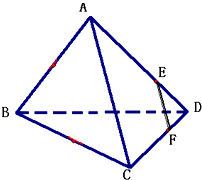在正四面体ABCD中，点F在CD上，点E在AD上，且DF：FC=DE：EA=2：3．证明：
（1）EF∥平面ABC；
（2）直线BD⊥直线EF．
函数y=f（x）为奇函数，且x∈[0，+∞）时，f（x）=x2-3x，则不等式
f(x)-f(-x)
x
＞0的解集为
 
．
下列命题中正确的是
 
．
①命题p：“?x∈R，x2-2≥0”的否定形式是￢p：?x∈R，x2-2＜0；
②若￢p是q的必要条件，则p是￢q的充分条件；
③“M＞N”是“(
3
4
)M＞(
3
4
)N”的充分不必要条件．
已知长方体的三边长分别是3，4，5，则它的外接球的表面积是
 
．
函数f（x）=log2（3+2x-x2）的单调递增区间为
 
．
若f（x）是定义在R上的函数，则“f（0）=0”是“函数f（x）为奇函数”的
 
条件（从“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选一个）．
计算下列各式的值：
（1）(
2
3
)-2+(1-
2
)0-(
27
8
)
2
3
；         
（2）
2lg2+lg3
1+
1
2
lg0.36+
1
3
lg8
．
关于函数f（x）=2
|x|
x2+1
，有下列命题：
①其图象关于y轴对称；
②f（x）在（-∞，0）上是增函数；
③f（x）的最大值为1；
④对任意a，b，c∈R，f（a），f（b），f（c）都可做为某一三角形的三边长．
其中正确的序号是（　　）
A、①③B、②③C、①④D、③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网