题目内容
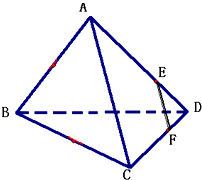 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:(1)EF∥平面ABC;
(2)直线BD⊥直线EF.
考点:直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)证明EF∥AC,利用直线与平面平行的判定定理,即可证明结论;
(2)取BD的中点M,连AM,CM,证明BD⊥平面AMC,可得BD⊥AC,利用HF∥AC,证明直线BD⊥直线EF.
(2)取BD的中点M,连AM,CM,证明BD⊥平面AMC,可得BD⊥AC,利用HF∥AC,证明直线BD⊥直线EF.
解答:
证明:(1)因为点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3,…(1分)
所以EF∥AC,…(3分)
又EF?平面ABC,
AC?平面ABC,
所以EF∥平面ABC.…(6分)
(2)取BD的中点M,连AM,CM,
因为ABCD为正四面体,所以AM⊥BD,CM⊥BD,…(8分)
又AM∩CM=M,所以BD⊥平面AMC,…(10分)
又AC?平面AMC,所以BD⊥EF,…(12分)
又EF∥AC,
所以直线BD⊥直线EF.…(14分)
所以EF∥AC,…(3分)
又EF?平面ABC,
AC?平面ABC,
所以EF∥平面ABC.…(6分)
(2)取BD的中点M,连AM,CM,
因为ABCD为正四面体,所以AM⊥BD,CM⊥BD,…(8分)
又AM∩CM=M,所以BD⊥平面AMC,…(10分)
又AC?平面AMC,所以BD⊥EF,…(12分)
又EF∥AC,
所以直线BD⊥直线EF.…(14分)
点评:本题考查直线与平面平行、垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a=log37,b=211,c=0.83.1,则( )
| A、b<a<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
已知两直线l1:x+my+3=0,l2:(m-1)x+2my+2m=0,若l1∥l2,则m的值为( )
| A、0 | ||
B、-1或
| ||
| C、3 | ||
| D、0或3 |
若a∈R,且loga(2a+1)<loga(3a)<0,则a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
 已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x
已知函数f(x)是定义在[-5,5]上的偶函数,且当x≤0时,f(x)=x2+4x