题目内容
若数列{an}的前n项和为Sn，数列{Sn}的前n项和为Tn=2n+1-n-2，则an= ．
考点：数列的求和
专题：等差数列与等比数列
分析：利用公式法求和即可．
解答：
解：∵Tn=2n+1-n-2，①
n=1时，a1=T1=22-1-2=1，
n≥2时，Tn-1=2n-（n-1）-2，②
由①-②得an=2n+1-2n-1=2n-1，
经检验上式对n=1时也成立，
∴an=2n-1．
故答案为：2n-1．
n=1时，a1=T1=22-1-2=1，
n≥2时，Tn-1=2n-（n-1）-2，②
由①-②得an=2n+1-2n-1=2n-1，
经检验上式对n=1时也成立，
∴an=2n-1．
故答案为：2n-1．
点评：本题主要考查利用公式an=sn-sn-1（n≥2）求数列的和，属于基础题．
练习册系列答案
相关题目
函数f（x）=
的值域是（ ）
| 8 |
| x2-4x+5 |
| A、（0，8] |
| B、（0，+∞） |
| C、[8，+∞） |
| D、（-∞，8] |
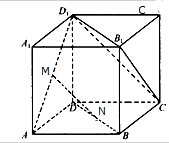如图所示，在正方体ABCD-A1B1C1D1中，已知正方体的棱长为