Question

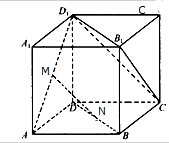如图所示，在正方体ABCD-A₁B₁C₁D₁中，已知正方体的棱长为

2

，M、N分别在AD₁与DB上，若AM=BN=x．求证：
（1）MN∥面CDD₁C₁；
（2）设MN=y，求y=f（x）的表达式；
（3）求MN的最小值及x的值．

Answer 1

考点：函数解析式的求解及常用方法,直线与平面平行的判定

专题：

分析：（1）运用坐标系判断证明．
（2）求出坐标，再求向量的模即可．
（3）运用函数求解．

解答： 解：（1）建立空间坐标系，以D原点，DA为x轴，DC为y轴，DD₁为z轴．
正方体的棱长为

2

，M、N分别在AD₁与DB上，若AM=BN=x．
D（0，0，0），A（

2

，0，0），M（

2

-

2

2

x，0.

2

2

x），N（

2

-

2

2

x，

2

-

2

2

x，0）

MN

=（0，

2

-

2

2

x，-

2

2

x），面CDD₁C₁的法向量为

n0

=（

2

，0，0），
∵

MN

•

n0

=0，M点不在平面CDD₁C₁内
∴，MN∥面CDD₁C₁；
（2）设MN=y，y=f（x）=

x2-2x+2

，x∈[0.

2

]
（3）f（x）=

x2-2x+2

=

(x-1)2+1

，x∈[0.

2

]
根据二次函数的单调性可知：x=1时，最小值为1

点评：本题考察了用坐标系解决几何问题．