题目内容
10．已知A（2，5，-6），点P在y轴上，|PA|=7，则点P的坐标是（ ）| A． | （0，8，0） | B． | （0，2，0） | C． | （0，8，0）或（0，2，0） | D． | （0，-8，0） |
分析 设出P的坐标，利用两点距离公式，求出P的坐标．
解答 解：由题意设P（0，y，0），
因为|PA|=7，
所以$\sqrt{4+（5-y）^{2}+36}$=7，
所以y=2或y=8，
所以点P的坐标为：（0，2，0）或（0，8，0）．
故选：C．
点评 本题考查空间两点间距离公式的应用，考查计算能力．
练习册系列答案
相关题目
20．sin20°sin80°-cos160°sin10°=（ ）
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $\frac{1}{2}$ |
18．设p：0＜x＜5，q：x2-4x-21＜0，那么p是q的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
5．已知函数f（x）=alnx的导函数是f′（x）且f′（2）=2，则实数的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | 4 |
15．化简 $\overrightarrow{AB}-\overrightarrow{CD}+\overrightarrow{BD}-\overrightarrow{AC}$的结果是（ ）
| A． | $\overrightarrow 0$ | B． | $\overrightarrow{AC}$ | C． | $\overrightarrow{BD}$ | D． | $\overrightarrow{DA}$ |
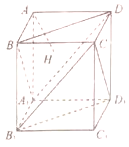如图，在正方体ABCD-A1B1C1D1中，过点A作平面A1BD的垂线，垂足为点H，给出以下命题：①H是△A1BD的垂心；②AH垂直于平面CB1D1；③AH的延长线过点C1；④直线AH和BB1所成角的大小为45°，其中正确的命题个数为（ ）
19．平面内到x轴与到y轴的距离之和为1的点的轨迹为（ ）
| A． | 点 | B． | 线段 | C． | 正方形 | D． | 圆 |