题目内容
2.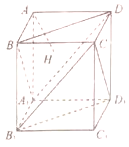 如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )
如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先,判断三棱锥 A-BA1D为正三棱锥,然后,得到△BA1D为正三角形,得到H为A在平面A1BD内的射影,然后,根据平面A1BD⊥平面BC1D,得到②正确,最后,结合线面角和对称性求解.
解答 解:∵AB=AA1=AD,BA1=BD=A1D,
∴三棱锥 A-BA1D为正三棱锥,
∴点H是△A1BD的垂心,故①为真命题;
∵平面A1BD与平面B1CD1平行,
∵AH⊥平面A1BD,
∵平面A1BD⊥平面BC1D,
∴AH垂直平面CB1D1,故②为真命题;
根据正方体的对称性得到AH的延长线经过C1,故③为真命题
∵AA1∥BB1,∴∠A1AH就是直线AH和BB1所成角,
在直角三角形AHA1中,
∵AA1=1,A1H=$\frac{2}{3}×\frac{\sqrt{3}}{2}×\sqrt{2}$=$\frac{\sqrt{6}}{3}$,
∴sin∠A1AH=$\frac{\sqrt{6}}{3}$,故④为假命题;
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了正方体的几何特征,线面垂直,直线与平面的夹角等知识点,难度中档.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
12.已知集合A={x||x|≤2},B={x|x2-2x-3≤0},则A∩B=( )
| A. | [-1,2] | B. | [-2,3] | C. | [-2,1] | D. | [1,2] |
13.已知平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都等于2,且两两夹角为60°,则对角线BD1的长度为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $\frac{{\sqrt{3}}}{2}+2$ |
10.已知A(2,5,-6),点P在y轴上,|PA|=7,则点P的坐标是( )
| A. | (0,8,0) | B. | (0,2,0) | C. | (0,8,0)或(0,2,0) | D. | (0,-8,0) |
17.已知一扇形的圆心角是60°,弧长是π,则这个扇形的面积是( )
| A. | 3π | B. | $\frac{3π}{2}$ | C. | 6π | D. | $\frac{3π}{4}$ |
14.函数f(x)=aex-sinx在x=0处有极值,则a的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | e |
11. 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
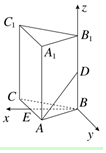 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.