题目内容
18.设p:0<x<5,q:x2-4x-21<0,那么p是q的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 q:x2-4x-21<0,解得-3<x<7,即可判断出结论.
解答 解:q:x2-4x-21<0,解得-3<x<7,
又p:0<x<5,
那么p是q的充分不必要条件.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.已知函数f(x)=e|x|,函数g(x)=$\left\{\begin{array}{l}{ex,x≤4}\\{4{e}^{5-x},x>4}\end{array}\right.$对任意的x∈[1,m](m>1),都有f(x-2)≤g(x),则m的取值范围是( )
| A. | (1,2+ln2] | B. | (1,$\frac{7}{2}$+ln2] | C. | [ln2,2) | D. | (2,$\frac{7}{2}$+ln2) |
13.已知平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都等于2,且两两夹角为60°,则对角线BD1的长度为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $\frac{{\sqrt{3}}}{2}+2$ |
3.约束条件为$\left\{\begin{array}{l}{x+y-5≤0}\\{x-y-k≤0}\\{x≥0,y≥0}\end{array}\right.$,目标函数Z=2x-y,则Z的最大值是( )
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
10.已知A(2,5,-6),点P在y轴上,|PA|=7,则点P的坐标是( )
| A. | (0,8,0) | B. | (0,2,0) | C. | (0,8,0)或(0,2,0) | D. | (0,-8,0) |
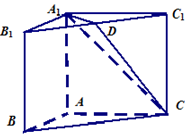 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题: