题目内容
1.点M,N是抛物线E上的两动点,M到点(2,0)的距离比到直线x+3=0的距离少1,点O(M,N与O不重合)是坐标原点,OM⊥ON.(Ⅰ)求抛物线E的标准方程;
(Ⅱ)在x轴上是否存在定点总在直线MN上,若存在,求出该定点的坐标;若不存在,请说明理由.
分析 (1)判断E是以点(2,0)为焦点,以x=-2为准线的抛物线,求出抛物线方程即可.
(2)设直线MN的方程为x=my+n,与x轴的交点为(n,0),M(x1,y1),N(x2,y2),联立直线与抛物线的方程组,通过韦达定理以及x1x2+y1y2=0,求出n,然后判断直线MN的方程为x=my+8,过定点(8,0)即可.
解答 解:(1)由题可得,E是以点(2,0)为焦点,以x=-2为准线的抛物线,
∴抛物线E的标准方程是:y2=8x;…(4分)
(2)设直线MN的方程为x=my+n,与x轴的交点为(n,0),M(x1,y1),N(x2,y2),
则$\left\{\begin{array}{l}{{y}^{2}=8x}\\{x=my+n}\end{array}\right.$,可得y2=8my+8n,即y2-8my-8n=0;…(6分)
又由OM⊥ON得:x1x2+y1y2=0,而x1x2=$\frac{{{y}_{1}}^{2}}{8}•\frac{{{y}_{2}}^{2}}{8}$=$\frac{({y}_{1}{y}_{2})^{2}}{64}$,y1y2=-8n,
∴$\frac{64{n}^{2}}{64}-8n=0$解得n=8,n=0(舍去),…(10分)
∴直线MN的方程为x=my+8,过定点(8,0),
即得在x轴上存在定点满足条件,其坐标是(8,0)…(12分)
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查计算能力.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
12.已知集合A={x||x|≤2},B={x|x2-2x-3≤0},则A∩B=( )
| A. | [-1,2] | B. | [-2,3] | C. | [-2,1] | D. | [1,2] |
6.已知函数f(x)=e|x|,函数g(x)=$\left\{\begin{array}{l}{ex,x≤4}\\{4{e}^{5-x},x>4}\end{array}\right.$对任意的x∈[1,m](m>1),都有f(x-2)≤g(x),则m的取值范围是( )
| A. | (1,2+ln2] | B. | (1,$\frac{7}{2}$+ln2] | C. | [ln2,2) | D. | (2,$\frac{7}{2}$+ln2) |
13.已知平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都等于2,且两两夹角为60°,则对角线BD1的长度为( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $\frac{{\sqrt{3}}}{2}+2$ |
10.已知A(2,5,-6),点P在y轴上,|PA|=7,则点P的坐标是( )
| A. | (0,8,0) | B. | (0,2,0) | C. | (0,8,0)或(0,2,0) | D. | (0,-8,0) |
11. 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
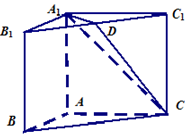 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题: