题目内容
17.已知等差数列{an}的公差不为零,且满足a1=6,a2,a6,a14成等比数列.(1)求数列{an}的通项公式;
(2)记bn=$\frac{2}{{(n+1){a_n}}}$,求数列{bn}的前n项和Sn.
分析 (1)设等差数列{an}的公差为d≠0,由a2,a6,a14成等比数列.可得${a}_{6}^{2}$=a2•a14,即(6+5d)2=(6+d)(6+13d),化简即可得出.
(2)bn=$\frac{2}{{(n+1){a_n}}}$=$\frac{2}{(n+1)(2n+4)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,利用“裂项求和”方法即可得出.
解答 解:(1)设等差数列{an}的公差为d≠0,∵a2,a6,a14成等比数列.∴${a}_{6}^{2}$=a2•a14,
∴(6+5d)2=(6+d)(6+13d),化为d2-2d=0,d≠0,解得d=2.
所以an=6+2(n-1)=2n+4.
(2)bn=$\frac{2}{{(n+1){a_n}}}$=$\frac{2}{(n+1)(2n+4)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,
∴数列{bn}的前n项和Sn═+$(\frac{1}{3}-\frac{1}{4})$+…+$(\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{1}{2}-\frac{1}{n+2}$=$\frac{n}{2(n+2)}$.
点评 本题考查了“裂项求和”方法、等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.已知A(2,5,-6),点P在y轴上,|PA|=7,则点P的坐标是( )
| A. | (0,8,0) | B. | (0,2,0) | C. | (0,8,0)或(0,2,0) | D. | (0,-8,0) |
11. 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
 利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量?
(注:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{x})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
2.若向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,-4),若$\overrightarrow{a}∥\overrightarrow{b}$则x=( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
6.直线x-$\sqrt{3}$y=3的倾斜角的大小为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
7.双曲线$\frac{x^2}{m}-{y^2}=1$的虚轴长是实轴长的2倍,则m=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{4}$ |
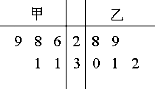 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论: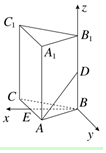 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为$\frac{\sqrt{6}}{4}$.