题目内容
f（x）=
-x+m有两个零点，则m∈ ．
| 4-x2 |
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：f（x）=
-x+m有两个零点，那么方程
-x+m=0有两根，构造函数y=
和y=x-m，这两个函数图象有两个交点，利用数形结合得到m的范围．
| 4-x2 |
| 4-x2 |
| 4-x2 |
解答：
解：由已知方程
-x+m=0有两根，构造函数y=
和y=x-m，这两个函数图象有两个交点，如图，
满足条件的2≤-m＜2
，所以-2
＜m≤-2；
故答案为：-2
＜m≤-2；
| 4-x2 |
| 4-x2 |
满足条件的2≤-m＜2
| 2 |
| 2 |
故答案为：-2
| 2 |
点评：本题考查了函数的零点与方程根以及函数图象交点之间的关系，利用了数形结合的方法，属于中档题．
练习册系列答案
相关题目
判断下列各组中的两个函数图象相同的是（ ）
①y1=
，y2=x-5；
②y1=
，y2=
；
③f（x）=x，g（x）=
；
④f1(x)=(
)2，f2（x）=2x．
①y1=
| (x+3)(x-5) |
| x+3 |
②y1=
| x+1 |
| x-1 |
| (x+1)(x-1) |
③f（x）=x，g（x）=
| x2 |
④f1(x)=(
| 2x |
| A、①、② | B、③ | C、④ | D、无 |
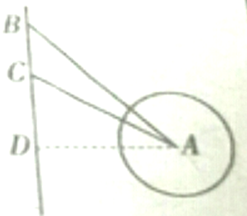某学校组织同学们参加红色七日游--还上夏令营活动，如图，海中小岛A周围20海里内有暗礁，夏令营的船只正向南航行，在B处测得小岛A在船的南偏东30°；航行30海里后，在C处测得小岛A在船的南偏东60°，如果此船不改变航向，继续向南航行，有无触礁危险？设
，
，
为单位向量，
，
的夹角为60°，则（
+
）•
的最大值为（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
椭圆：
+
=1（a＞b＞0）上存在点P使
•
＜0，则离心率e∈（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（0，
| ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
已知A（-2，0），B（2，0）为坐标平面上两个定点，动点M在x轴上的射影为N，且满足|MN|2=4|AN|•|BN|．