题目内容
某药厂测试一种新药的疗效,随机选择600名志愿者服用此药,结果如下:
(1)若另有一病人服用此药,请估计该病人病情好转的概率;
(2)现从服用此药的600名志愿者中选择6人作进一步数据分析,若在三种疗效的志愿者中各取2人,这种抽样是否合理?若不合理,应该如何抽样?(请写出具体人数安排)
(3)在选出作进一步数据分析的6人中,任意抽取2人参加药品发布会,求抽取的2人中有病情恶化的志愿者的概率.
| 治疗效果 | 病情好转 | 病情无明显变化 | 病情恶化 |
| 人数 | 400 | 100 | 100 |
(2)现从服用此药的600名志愿者中选择6人作进一步数据分析,若在三种疗效的志愿者中各取2人,这种抽样是否合理?若不合理,应该如何抽样?(请写出具体人数安排)
(3)在选出作进一步数据分析的6人中,任意抽取2人参加药品发布会,求抽取的2人中有病情恶化的志愿者的概率.
考点:古典概型及其概率计算公式,频率分布表
专题:概率与统计
分析:(1)利用表中数据直接计算即可;
(2)根据随机抽样的概念可以判断这种抽样不合理,可以采用分层抽样解决;
(3)列举6人中任意抽取2人的所有基本事件,找出2人中有病情恶化的基本事件,利用古典概型概率公式计算即可.
(2)根据随机抽样的概念可以判断这种抽样不合理,可以采用分层抽样解决;
(3)列举6人中任意抽取2人的所有基本事件,找出2人中有病情恶化的基本事件,利用古典概型概率公式计算即可.
解答:
解:(1)由已知统计表可知在600个病人中,
服药后出现病情好转的频率为
=
,
∴估计另一个病人服用此药病情好转的概率为
.
(2)在三种疗效的志愿者中各取2人,这种抽样不合理,
由于用药后人治疗效果之间存在明显差异,
∴要进一步抽样则应该按照治疗效果进行分层抽样,
即从病情好转的志愿者中抽4人,
从病情无明显变化的志愿者中抽1人,
从病情恶化的志愿者中抽1人组成6人样本,
(3)将6人中病情恶化的1人用符号A代替,其余5人用分别用符号1,2,3,4,5代替,
则从6人中任意抽取2人的基本事件表示如下:(1,2),(1,3),(1,4),(1,5),
(1,A),(2,3),(2,4),(2,5),(2,A),(3,4),(3,5),(3,A),(4,5),
(4,A),(5,A),
一共15个基本事件,
其中抽到病情恶化志愿者的基本事件为:(1,A),(2,A),(3,A),(4,A),(5,A)
一共5个基本事件,
∵每个基本事件是等可能的,
根据古典概型可得,抽取2人中有病情恶化的志愿者的概率为
=
.
服药后出现病情好转的频率为
| 400 |
| 600 |
| 2 |
| 3 |
∴估计另一个病人服用此药病情好转的概率为
| 2 |
| 3 |
(2)在三种疗效的志愿者中各取2人,这种抽样不合理,
由于用药后人治疗效果之间存在明显差异,
∴要进一步抽样则应该按照治疗效果进行分层抽样,
即从病情好转的志愿者中抽4人,
从病情无明显变化的志愿者中抽1人,
从病情恶化的志愿者中抽1人组成6人样本,
(3)将6人中病情恶化的1人用符号A代替,其余5人用分别用符号1,2,3,4,5代替,
则从6人中任意抽取2人的基本事件表示如下:(1,2),(1,3),(1,4),(1,5),
(1,A),(2,3),(2,4),(2,5),(2,A),(3,4),(3,5),(3,A),(4,5),
(4,A),(5,A),
一共15个基本事件,
其中抽到病情恶化志愿者的基本事件为:(1,A),(2,A),(3,A),(4,A),(5,A)
一共5个基本事件,
∵每个基本事件是等可能的,
根据古典概型可得,抽取2人中有病情恶化的志愿者的概率为
| 5 |
| 15 |
| 1 |
| 3 |
点评:本题考查样本估计总体、分层抽样、古典概型概率计算等基础知识的综合应用,属于中档题.

练习册系列答案
相关题目
已知f(x)是定义在(0,+∞)上的单调函数,f′(x)是f(x)的导函数,若对?x∈(0,+∞),都有f[f(x)-2x]=3,则方程f′(x)-
=0的解所在的区间是( )
| 4 |
| x |
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,3) |
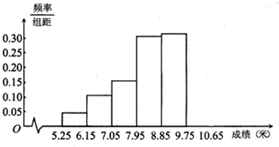 把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.
把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格. 如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.
如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.