题目内容
设0＜a＜b，且f（x）=
，则下列大小关系式成立的是（ ）
1+
| ||
| x |
A、f （a）＜f （
| ||||
B、f （
| ||||
C、f （
| ||||
D、f （b）＜f （
|
考点：函数单调性的性质,基本不等式
专题：计算题,函数的性质及应用
分析：明确f（x）=
在（0，+∞）上是单调减函数，再由基本不等式明确b＞
＞
，利用函数的单调性定义来求解．
1+
| ||
| x |
| a+b |
| 2 |
| ab |
解答：
解：∵0＜a＜b，
∴b＞
＞
又∵f（x）=
，
∴f′（x）=
=
＜0，
∴f（x）=
在（0，+∞）上是单调减函数，
∴f （b）＜f （
）＜f （
）
故选：D．
∴b＞
| a+b |
| 2 |
| ab |
又∵f（x）=
1+
| ||
| x |
∴f′（x）=
| ||||||
| x2 |
-x-2-2
| ||
2
|
∴f（x）=
1+
| ||
| x |
∴f （b）＜f （
| a+b |
| 2 |
| ab |
故选：D．
点评：本题主要考查指数函数的单调性和基本不等式．解答的关键是在比较大小时体现了函数思想．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
一个由三个正方体组成几何体的三视图如图所示，则该几何体的体积为（ ）
A、9+2
| ||
| B、11 | ||
| C、9.125 | ||
D、10+2
|
设全集U=R，集合A={x|x2-1＜0}，B={x|x+2≥0}，则A∩B=（ ）
| A、A |
| B、B |
| C、{x|-2≤x＜1} |
| D、{x|-1＜x≤2} |
已知f（x）是定义在（0，+∞）上的单调函数，f′（x）是f（x）的导函数，若对?x∈（0，+∞），都有f[f（x）-2x]=3，则方程f′（x）-
=0的解所在的区间是（ ）
| 4 |
| x |
A、（0，
| ||
B、（
| ||
| C、（1，2） | ||
| D、（2，3） |
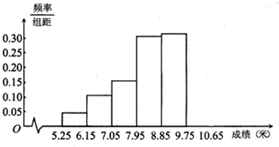把参加某次铅球投掷的同学的成绩（单位：米）进行整理，分成以下6个小组：[5.25，6.25），[6.15，7.05），[7.05，7.95），[7.95，8.85），[8.85，9.75），[9.75，10.65），并绘制出频率分布直方图，如图所示的是这个频率分布直方图的一部分．已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30，第6小组的频数是7．规定：投掷成绩不小于7.95米的为合格．