题目内容
12.已知等差数列{an}的公差为d,等比数列{bn}的公比为q,设{an},{bn}的前n项和分别为Sn,Tn,若${n^2}({T_n}+1)={2^n}{S_n}$,n∈N*,则d=2,q=2.分析 在已知等式中分别取n=1、2、3、4,得到关于a1,b1,d,q的方程组,求解得答案.
解答 解:由${n^2}({T_n}+1)={2^n}{S_n}$,得
b1+1=2a1,b1+b1q+1=2a1+d,
$9({b}_{1}+{b}_{1}q+{b}_{1}{q}^{2}+1)=8(3{a}_{1}+3d)$,${b}_{1}+{b}_{1}q+{b}_{1}{q}^{2}+{b}_{1}{q}^{3}=4{a}_{1}+6d$.
联立以上各式解得:d=q=2.
故答案为:2,2.
点评 本题考查等差数列和等比数列的通项公式及前n项和公式,考查计算求解能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.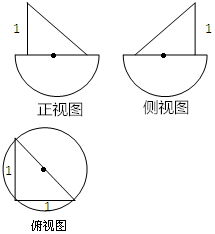 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )| A. | 1+$\frac{\sqrt{3}+3π}{2}$ | B. | $\frac{1+\sqrt{3}+π}{2}$ | C. | $\frac{1+\sqrt{3}+3π}{2}$ | D. | $\frac{3+\sqrt{3}+3π}{2}$ |
17.已知全集U={x|x≤9,x∈N+},集合A={1,2,3},B={3,4,5,6},则∁U(A∪B)=( )
| A. | {3} | B. | {7,8} | C. | {7,8,9} | D. | {1,2,3,4,5,6} |
4.函数$f(x)={(\frac{1}{2})^{\sqrt{x-{x^2}}}}$的单调递增区间为( )
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{0,\frac{1}{2}}]$ | C. | $[\frac{1}{2},+∞)$ | D. | $[{\frac{1}{2},1}]$ |
1.f(x)为奇函数,当x>0时,f(x)=π-arccos(sinx)则x<0时,f(x)=( )
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
2.已知直线l与椭圆C:$\frac{x^2}{4}+{y^2}=1$交于A,B两点,且|AB|=2,则直线l与圆x2+y2=1的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相交或相切 |
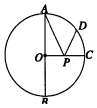 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.