题目内容
20.函数f(x)=$\frac{x^2+a}{x+1}(a∈R)$(Ⅰ)若f(x)在点(1,f(1))处的切线斜率为$\frac{1}{2}$,求实数a的值;
(Ⅱ)若f(x)在x=1处取得极值,求函数f(x)的单调区间.
分析 (Ⅰ)求出函数的导数,求出切线的斜率,即可求解实数a的值;
(Ⅱ)利用极值点求出a,求出函数的导数,利用导函数的符号,求解单调区间.
解答 解:(Ⅰ)函数f(x)=$\frac{x^2+a}{x+1}(a∈R)$,
${f^'}(x)=\frac{{{x^2}+2x-a}}{{{{(x+1)}^2}}}$,
∵f(x)在点(1,f(1))处的切线斜率为$\frac{1}{2}$,
∴${f^'}(1)=\frac{1}{2},解得a=1$…(4分).
(Ⅱ)∵f(x)在x=1处取得极值,∴f′(1)=0,解得a=3,
∴${f^'}(x)=\frac{{{x^2}+2x-3}}{{{{(x+1)}^2}}}$(x≠-1)…(6分)
由f′(x)>0,解得x<-3或x>1;
由f′(x)<0,解得-3<x<1且x≠-1;
所以f(x)的单调增区间是(-∞,-3)和(1,+∞),
单调减区间是(-3,-1)和(-1,1).…10分
点评 本题考查函数的导数的应用,单调区间以及切线方程的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
10.已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
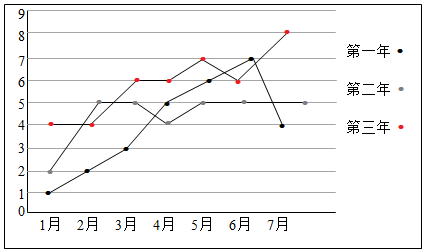
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
相关公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.

(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
11.若点P为△ABC某两边的垂直平分线的交点,且$\overrightarrow{PA}+\overrightarrow{PB}-\overrightarrow{PC}=\overrightarrow 0$,则∠ACB=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
8.已知数列{an}满足an+1=an+3,a1=0,则数列{an}的通项公式可以是( )
| A. | n | B. | 2n | C. | 3n-3 | D. | 3n+3 |
12.已知等差数列{an}的公差为d,等比数列{bn}的公比为q,设{an},{bn}的前n项和分别为Sn,Tn,若${n^2}({T_n}+1)={2^n}{S_n}$,n∈N*,则d=2,q=2.
10.已知集合A={-1,0,1},B={x|x=sin$\frac{2k+1}{x}$,k∈Z},则∁AB=( )
| A. | ∅ | B. | 0 | C. | {0} | D. | {-1,1} |