题目内容
2.在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别为A1B1,B1C1的中点,则直线BE与直线CF所成角的余弦值是$\frac{\sqrt{30}}{10}$.分析 以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,由此能求出直线BE与直线CF所成角的余弦值.
解答 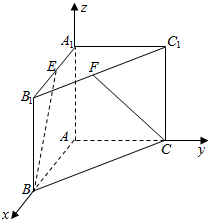 解:∵在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别为A1B1,B1C1的中点,
解:∵在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别为A1B1,B1C1的中点,
∴以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
B(2,0,0),E(1,0,2),C(0,2,0),B1(2,0,2),C1(0,2,2),F(1,1,2),
$\overrightarrow{BE}$=(-1,0,2),$\overrightarrow{CF}$=(1,-1,2),
设异面直线BE与直线CF所成角为θ,
则cosθ=$\frac{|\overrightarrow{BE}•\overrightarrow{CF}|}{|\overrightarrow{BE}|•|\overrightarrow{CF}|}$=$\frac{3}{\sqrt{5}•\sqrt{6}}$=$\frac{\sqrt{30}}{10}$.
∴直线BE与直线CF所成角的余弦值是$\frac{\sqrt{30}}{10}$.
故答案为:$\frac{{\sqrt{30}}}{10}$.
点评 本题考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.设a>b>0,则下列不等式恒成立的为( )
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
10.已知命题p:若x∈N*,则x∈Z.命题q:?x0∈R,${(\frac{1}{2})^{x_0}}=0$.则下列命题为真命题的是( )
| A. | ¬p | B. | p∧q | C. | ¬p∨q | D. | ¬p∨¬q |
7.“平面内一动点P到两个定点的距离的和为常数”是“平面内一动点P的轨迹为椭圆”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.如果集合A={x|mx2-4x+2=0}中只有一个元素,则实数m的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
12.下列方程中,表示圆的方程的是( )
| A. | x2+2x+y2-4y+7=0 | B. | $\left\{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}\right.$(0≤θ≤2π) | ||
| C. | ρ=5cosθ | D. | ρ2cos2θ=1 |