题目内容
11.设函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,其中向量$\overrightarrow{a}$=(m,cos2x),$\overrightarrow{b}$=(1+sin2x,1),且y=f(x)的图象经过点$({\frac{π}{4},2})$,则实数m的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出f(x)解析式,将点$({\frac{π}{4},2})$代入f(x)列方程解出m.
解答 解:f(x)=m(1+sin2x)+cos2x,∵y=f(x)的图象经过点$({\frac{π}{4},2})$,∴m(1+1)+0=2,解得m=1.
故选:A.
点评 本题考查了平面向量的数量积运算,特殊角的三角函数值,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
2.在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别为A1B1,B1C1的中点,则直线BE与直线CF所成角的余弦值是$\frac{\sqrt{30}}{10}$.
6.已知a<b<0,则下列不等式成立的是( )
| A. | a2<b2 | B. | $\frac{a}{b}<1$ | C. | a<1-b | D. | $\frac{1}{a}<\frac{1}{b}$ |

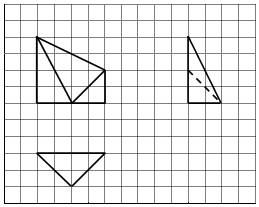 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )