题目内容
12.下列方程中,表示圆的方程的是( )| A. | x2+2x+y2-4y+7=0 | B. | $\left\{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}\right.$(0≤θ≤2π) | ||
| C. | ρ=5cosθ | D. | ρ2cos2θ=1 |
分析 A.原方程配方化为:(x+1)2+(y-2)2=-2,即可判断出结论;
B.利用cos2θ+sin2θ=1化为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1,即可判断出图形;
C.ρ=5cosθ化为ρ2=5ρcosθ,化为x2+y2=5x,配方即可判断出图形.
D.ρ2cos2θ=1,化为x2-y2=1,即可判断出图形.
解答 解:A.x2+2x+y2-4y+7=0,配方化为:(x+1)2+(y-2)2=-2,不表示任何图形;
B.$\left\{\begin{array}{l}{x=3cosθ}\\{y=4sinθ}\end{array}\right.$(0≤θ≤2π),化为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{16}$=1,表示焦点在y轴上的椭圆;
C.ρ=5cosθ化为ρ2=5ρcosθ,化为x2+y2=5x,化为$(x-\frac{5}{2})^{2}+{y}^{2}$=$\frac{25}{4}$,表示以$(\frac{5}{2},0)$为圆心,$\frac{5}{2}$为半径的圆.
D.ρ2cos2θ=1,化为x2-y2=1,表示焦点在x轴上的等轴双曲线.
故选:C.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
2.在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E,F分别为A1B1,B1C1的中点,则直线BE与直线CF所成角的余弦值是$\frac{\sqrt{30}}{10}$.
17.函数y=$\frac{x}{{e}^{x}}$在[0,2]上的最大值是( )
| A. | $\frac{1}{e}$ | B. | $\frac{2}{{e}^{2}}$ | C. | 0 | D. | $\frac{1}{2\sqrt{e}}$ |
 在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
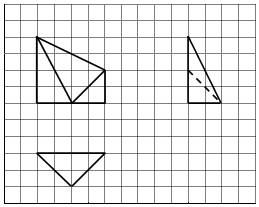 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )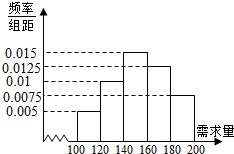 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小季给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.