题目内容
10.已知命题p:若x∈N*,则x∈Z.命题q:?x0∈R,${(\frac{1}{2})^{x_0}}=0$.则下列命题为真命题的是( )| A. | ¬p | B. | p∧q | C. | ¬p∨q | D. | ¬p∨¬q |
分析 先判定命题p与q的真假,再利用复合命题真假的判定方法即可得出.
解答 解:命题p:若x∈N*,则x∈Z.是真命题.
命题q:∵?x∈R,则$(\frac{1}{2})^{x}$>0,因此不?x0∈R,${(\frac{1}{2})^{x_0}}=0$.是假命题.
则下列命题为真命题的是¬p∨¬q.
故选:D.
点评 本题考查了复合命题真假的判定方法、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.已知M={(x,y)|x2+2y2=3},N={(x,y)|y=mx+b}.若对于所有的m∈R,均有M∩N≠∅,则b的取值范围是( )
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
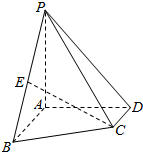 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.