题目内容
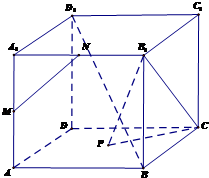如图，已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，（1）求证：MN∥平面PB1C．
（2）求证：D1B⊥平面PB1C．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）利用线面平行的判定定理即可证明；
（2）证明PB1⊥D1B，AC⊥D1B，利用线面垂直的判定定理即可证明．
（2）证明PB1⊥D1B，AC⊥D1B，利用线面垂直的判定定理即可证明．
解答：
证明：（1）连接AC，则AC一定过点P，连接AB1．
∵A1M=MA，A1N=NB1，∴MN∥AB1．
又MN?平面AB1C，AB1?平面AB1C，
∴MN∥平面AB1C，即MN∥平面PB1C．
（2）连D1B1，PB，
∵
=
=
，∠D1DB=∠PBB1=90°，
∴△D1DB∽△PBB1，
∴∠D1DB=∠BB1P，
∵∠PBB1=90°，
∴∠B1PB+∠D1BD=90°，
∴PB1⊥D1B①
∴B1B⊥平面ABCD，
∵AC?平面ABCD，
∴B1B⊥AC，
∵AC⊥BD，BD∩B1B=B，
∴AC⊥平面B1D
∵BD1?平面B1D，
∴AC⊥D1B②
∵PB1∩AC=P以及 ①②得：D1B⊥平面PB1C．
证明：（1）连接AC，则AC一定过点P，连接AB1．∵A1M=MA，A1N=NB1，∴MN∥AB1．
又MN?平面AB1C，AB1?平面AB1C，
∴MN∥平面AB1C，即MN∥平面PB1C．
（2）连D1B1，PB，
∵
| D1D |
| DB |
| PB |
| BB1 |
| 1 | ||
|
∴△D1DB∽△PBB1，
∴∠D1DB=∠BB1P，
∵∠PBB1=90°，
∴∠B1PB+∠D1BD=90°，
∴PB1⊥D1B①
∴B1B⊥平面ABCD，
∵AC?平面ABCD，
∴B1B⊥AC，
∵AC⊥BD，BD∩B1B=B，
∴AC⊥平面B1D
∵BD1?平面B1D，
∴AC⊥D1B②
∵PB1∩AC=P以及 ①②得：D1B⊥平面PB1C．
点评：熟练掌握线面平行、垂直的判定定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
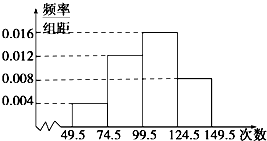为了了解小学生的体能情况，抽取了某小学同年级部分学生进行跳绳测试，将所得数据整理后，画出频率分布直方图如图所示，已知如图：第一小组的频数为5．
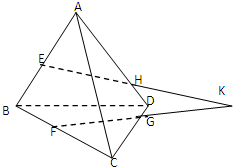如图，三棱锥A-BCD中，E、F分别是棱AB、BC的中点，H、G分别是棱AD、CD上的点，且EH∩FG=K．求证：