题目内容
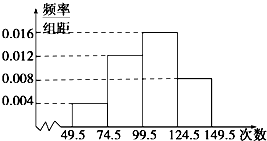 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.(1)求第四小组的频率;
(2)参加这次测试的学生人数是多少?
(3)估算学生这次跳绳次数的中位数与平均数.
考点:频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(1)由已知中从左到右前三个小组的频率分别是0.1,0.3,0.4,结合四组频率和为1,即可得到第四小组的频率;
(2)由已知中第一小组的频数为5及第一组频率为0.1,代入样本容量=
,即可得到参加这次测试的学生人数;
(3)由(2)的结论,我们可以求出第一、第二、第三、第四小组的频数,再结合中位数的定义,可求估算出数据的中位数,进而累加各组的频率与组中的积,可估算出数据的平均数.
(2)由已知中第一小组的频数为5及第一组频率为0.1,代入样本容量=
| 频数 |
| 频率 |
(3)由(2)的结论,我们可以求出第一、第二、第三、第四小组的频数,再结合中位数的定义,可求估算出数据的中位数,进而累加各组的频率与组中的积,可估算出数据的平均数.
解答:
 解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2.
解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2.
(2)设参加这次测试的学生人数是n,则有
n=
=5÷0.1=50(人).
(3)因为0.1×50=5,0.3×50=15,0.4×50=20,0.2×50=10,
即第一、第二、第三、第四小组的频数分别为5、15、20、10,
所以学生跳绳次数的中位数落在第三小组内.
中位数约为:99.5+
×(124.5-99.5)=105.75,
平均数约为:62×0.1+87×0.3+112×0.4+137×0.2=104.5
 解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2.
解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2.(2)设参加这次测试的学生人数是n,则有
n=
| 频数 |
| 频率 |
(3)因为0.1×50=5,0.3×50=15,0.4×50=20,0.2×50=10,
即第一、第二、第三、第四小组的频数分别为5、15、20、10,
所以学生跳绳次数的中位数落在第三小组内.
中位数约为:99.5+
| 5 |
| 20 |
平均数约为:62×0.1+87×0.3+112×0.4+137×0.2=104.5
点评:本题考查的知识点是中位数,频率颁布直方图,其中熟练掌握频率颁布直方图的画法及频率颁布直方图的用法,是解答本题的关键.

练习册系列答案
相关题目
已知等比数列{an}的前3项分别为4、6、x,则x为 ( )
| A、7 | B、8 | C、9 | D、10 |
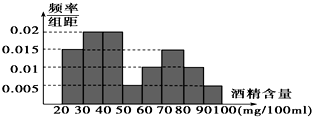 据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.
据《扬子晚报》报道,2013年8月1日至8月28日,某市交管部门共抽查了1000辆车,查出酒后驾车和醉酒驾车的驾驶员80人,图示是对这80人血液中酒精含量进行检查所得结果的频率分布直方图.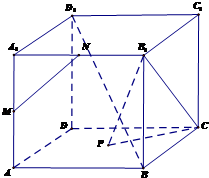 如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,
如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,