题目内容
用导数的定义求：
（1）y=
在x=1处的导数；
（2）y=x2+ax+b（a，b为常数）在x=-1处的导数．
（1）y=
| 2 |
| x2 |
（2）y=x2+ax+b（a，b为常数）在x=-1处的导数．
考点：导数的运算
专题：导数的概念及应用
分析：（1）根据题意进行分析，从1到1+△x时，曲线的增量为△y，则根据
的意义即可求得答案；
（2）根据题意进行分析，从-1到-1+△x时，曲线的增量为△y，则根据
的意义即可求得答案．
| lim |
| △x→0 |
| △y |
| △x |
（2）根据题意进行分析，从-1到-1+△x时，曲线的增量为△y，则根据
| lim |
| △x→0 |
| △y |
| △x |
解答：
解：（1）由于
=
=
=
=-4，
则y=
在x=1处的导数为-4；
（2）由于
=
=
=
（a-2+△x）=a-2，
则y=x2+ax+b（a，b为常数）在x=-1处的导数为a-2．
| lim |
| △x→0 |
| △y |
| △x |
=
| lim |
| △x→0 |
| ||||
| △x |
=
| lim |
| △x→0 |
| 2-2(1+△x)2 |
| △x(1+△x)2 |
=
| lim |
| △x→0 |
| -4-2△x |
| (1+△x)2 |
则y=
| 2 |
| x2 |
（2）由于
| lim |
| △x→0 |
| △y |
| △x |
=
| lim |
| △x→0 |
| (-1+△x)2+a×(-1+△x)+b-((-1)2+a×(-1)+b) |
| △x |
=
| lim |
| △x→0 |
| -2△x+(△x)2+a△x |
| △x |
=
| lim |
| △x→0 |
则y=x2+ax+b（a，b为常数）在x=-1处的导数为a-2．
点评：本题考查变化率与导数的基本意义，以及极限的运算，同时考查了运算能力，看清题中条件即可．属基础题．
练习册系列答案
相关题目
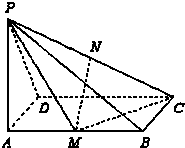如图，已知PA⊥矩形ABCD所在的平面，M、N分别为AB、PC的中点，∠PDA=45°，AB=2，AD=1
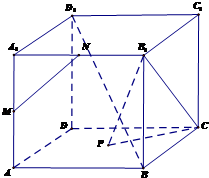如图，已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，
在如图所示的几何体中，四边形ABCD为正方形，△ABE为等腰直角三角形，∠BAE=90°，且AD⊥AE．