题目内容
对变量x,y,测得一组数据如下表:
(1)求变量x与y之间的相关系数(保留四个有效数字),并判断是否具有线性相关关系?是正相关还是负相关?(参考数据
≈5.385)
(2)若变量x与y之间具有线性相关关系,求y对x的线性回归方程
=bx+
.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| 29 |
(2)若变量x与y之间具有线性相关关系,求y对x的线性回归方程
 |
| y |
 |
| a |
考点:线性回归方程
专题:概率与统计
分析:(1)求出x和y的平均数,
,
,
xiyi,代入相关系数公式,可求出变量x与y之间的相关系数,进而根据相关系数的符号,判断是正相关还是负相关;
(2)将(1)中所得数据,利用最小二乘法,求出回归系数,可得y对x的线性回归方程
=bx+a
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| y | 2 i |
| 5 |
 |
| i=1 |
(2)将(1)中所得数据,利用最小二乘法,求出回归系数,可得y对x的线性回归方程
 |
| y |
解答:
解:(1)据此表知
=
(2+4+5+6+8)=5,
=
(20+40+60+70+80)=54,
=145,
=16900,
xiyi=1560;
∴sx=2,sy=4
,sxy=42,rxy≈0.9749>0,
故变量x与y之间具有线性相关关系,是正相关
(2)∵b=
=
=
=10.5,
a=
-10.5
=54-10.5×5=1.5,
∴y对x的回归直线方程为
=10.5x+1.5.
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| y | 2 i |
| 5 |
 |
| i=1 |
∴sx=2,sy=4
| 29 |
故变量x与y之间具有线性相关关系,是正相关
(2)∵b=
| |||||||
|
| 1560-5×5×54 |
| 145-5×52 |
| 210 |
| 20 |
a=
. |
| y |
. |
| x |
∴y对x的回归直线方程为
| ? |
| y |
点评:本题考查线性回归方程,是一个基础题,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.
已知正方形ABCD的边长为4,E,F分别是AB,AD的中点,GC⊥平面ABCD,GC=2,求三棱锥B-EFG的高.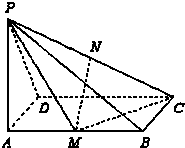 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1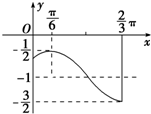 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.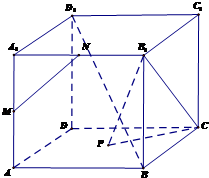 如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,
如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,