题目内容
已知角α终边落在射线3x+4y=0（x＜0）上，求
的值．
| sin(π-α)cos(3π+α)tanα |
| cos(-α)sin(π+α) |
考点：运用诱导公式化简求值,任意角的三角函数的定义
专题：三角函数的求值
分析：先运用诱导公式化简，然后在射线3x+4y=0（x＜0）上取点（a，-
），利用三角函数的定义可得结论．
| 3a |
| 4 |
解答：
解：
=
=tanα，
在射线3x+4y=0（x＜0）上取点（a，-
），
由三角函数的定义，则tanα=
=-
．
故
的值为：-
．
| sin(π-α)cos(3π+α)tanα |
| cos(-α)sin(π+α) |
=
| -sinαcosαtanα |
| -cosαsina |
=tanα，
在射线3x+4y=0（x＜0）上取点（a，-
| 3a |
| 4 |
由三角函数的定义，则tanα=
-
| ||
| a |
| 3 |
| 4 |
故
| sin(π-α)cos(3π+α)tanα |
| cos(-α)sin(π+α) |
| 3 |
| 4 |
点评：本题主要考察运用诱导公式化简求值，任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，若a1=-3，ak+1=
，Sk=-12，则正整数k=（ ）
| 3 |
| 2 |
| A、10 | B、11 | C、12 | D、13 |
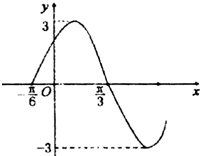
如图所示是y=Asin（ωx+φ）的图象（其中A＞0，ω＞0，|φ|≤
）一部分，则其解析表达式为（ ）
| π |
| 2 |
A、y=3cos（2x+
| ||
B、y=3cos（2x-
| ||
C、y=3sin（2x+
| ||
D、y=3sin（2x-
|
已知集合M={（x，y）|x+y＜0，xy＞0}，N={（x，y）|x＜0，y＜0}，那么（ ）
| A、N?M | B、M?N |
| C、M=N | D、M?N |
使函数y=sin（2x+θ）+
cos（2x+θ）在[-
，0]上是减函数的θ的一个值为（ ）
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|