题目内容
关于方程|log2x|=lg（x+1）的两个根x1，x2（x1＜x2）以下说法正确的是（ ）
| A、x1+x2＞2 |
| B、x1x2＞2 |
| C、0＜x1x2＜1 |
| D、1＜x1+x2＜2 |
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：在同一坐标系中作出y=|log2x|与y=lg（x+1）的图象，观察图象可得．
解答：
解：在同一坐标系中作出y=|log2x|与y=lg（x+1）的图象，如图：
由图可知：0＜x1＜1，1＜x2＜2，
所以1＜x1+x2＜2．
故选D．
解：在同一坐标系中作出y=|log2x|与y=lg（x+1）的图象，如图：由图可知：0＜x1＜1，1＜x2＜2，
所以1＜x1+x2＜2．
故选D．
点评：本题以基本初等函数为载体，考查了方程根与函数零点等问题，属于中档题．熟练运用函数的图象，将方程问题化为直观图象的观察，是解决本题的捷径．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=ax3-6ax2+b（a＞0）在区间[-1，2]上的最大值为3，最小值为-29，则（ ）
| A、a=2，b=-29 |
| B、a=3，b=2 |
| C、a=2，b=3 |
| D、以上都不对 |
要得到函数y=
cosx的图象，只需将函数y=
cos（2x+
）的图象上所有的点（ ）
| 2 |
| 2 |
| π |
| 4 |
A、横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标缩短到原来的
| ||||
D、横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动
|
如图所示是y=Asin（ωx+φ）的图象（其中A＞0，ω＞0，|φ|≤
）一部分，则其解析表达式为（ ）
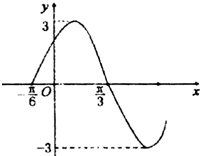
| π |
| 2 |
A、y=3cos（2x+
| ||
B、y=3cos（2x-
| ||
C、y=3sin（2x+
| ||
D、y=3sin（2x-
|
函数y=f（x）在区间（-2，2）上的图象是连续不断的，且方程f（x）=0在（-2，2）上仅有一个实根x=0，则f（-1）f（1）的值（ ）
| A、大于0 |
| B、小于0 |
| C、等于0 |
| D、与0的大小关系无法确定 |
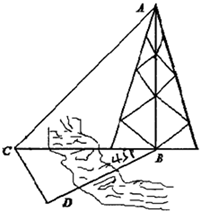如图，测量河对岸的塔的高度AB，可以选择与B在同一水平面内的两个点C、D．测得由C望A的仰角∠ACB=45°，方位角∠BCD═60°、∠BDC=75°，又测得C、D相距20米．试求塔的高度AB．