题目内容
已知集合A={x|x2-2x-8＜0}，B={x|x2＜a2}（其中a为正的常数），I=R，若A∩B=∅，则a的取值范围是 ．
考点：交集及其运算
专题：集合
分析：先求出集合A，B，根据A∩B=∅便可得到限制a的不等式，解不等式即得a的取值范围．
解答：
解：A=（-2，4），B=（-a，a）；
∵A∩B=∅；
∴4≤-a，或a≤-2；
∴a≤-2；
∴a的取值范围是（-∞，-2]．
故答案为：（-∞，-2]．
∵A∩B=∅；
∴4≤-a，或a≤-2；
∴a≤-2；
∴a的取值范围是（-∞，-2]．
故答案为：（-∞，-2]．
点评：考查解一元二次不等式，交集的概念，以及空集的概念．
练习册系列答案
相关题目
已知函数f（x）=
（x∈R）．
（1）求函数f（x）的值域；
（2）①判断并证明函数f（x）的奇偶性；②判断并证明函数f（x）的单调性；
（3）解不等式f（1-m）+f（1-m2）＜0．
| 2x-1 |
| 2x+1 |
（1）求函数f（x）的值域；
（2）①判断并证明函数f（x）的奇偶性；②判断并证明函数f（x）的单调性；
（3）解不等式f（1-m）+f（1-m2）＜0．
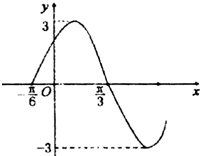
如图所示是y=Asin（ωx+φ）的图象（其中A＞0，ω＞0，|φ|≤
）一部分，则其解析表达式为（ ）
| π |
| 2 |
A、y=3cos（2x+
| ||
B、y=3cos（2x-
| ||
C、y=3sin（2x+
| ||
D、y=3sin（2x-
|