题目内容
某设备的使用年限x与所支出的总费用y(万元)统计数据如下表
据上表可得回归方程
=
x+
中的
=0.7,据此预测设备使用年限为6年时总费用为( )
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、4.95万元 |
| B、5.2万元 |
| C、4.35万元 |
| D、4.9万元 |
考点:线性回归方程
专题:计算题,概率与统计
分析:首先求出所给数据的平均数,得到样本中心点,根据线性回归直线过样本中心点,求出方程中的一个系数,得到线性回归方程,把自变量为7代入,预报出结果.
解答:
解:∵
=
(1+2+3+4)=2.5,
=
(1.5+2+3+3.5)=2.5,
∵数据的样本中心点在线性回归直线上,回归方程程
=
x+
中的
=0.7,
∴2.5=0.7×2.5+a,
∴a=-1.5,
∴线性回归方程是
=0.7x-1.5,
∴预测设备使用年限为6年时总费用为
=0.7×6-1.5=2.7万元,
故选:A.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
∵数据的样本中心点在线性回归直线上,回归方程程
 |
| y |
 |
| b |
 |
| a |
 |
| b |
∴2.5=0.7×2.5+a,
∴a=-1.5,
∴线性回归方程是
 |
| y |
∴预测设备使用年限为6年时总费用为
 |
| y |
故选:A.
点评:本题考查求回归方程,考查利用回归方程进行预测,解题的关键是根据回归方程必过样本中心点,求出回归系数.

练习册系列答案
相关题目
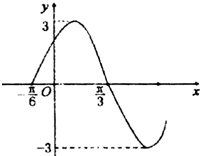
如图所示是y=Asin(ωx+φ)的图象(其中A>0,ω>0,|φ|≤
)一部分,则其解析表达式为( )
| π |
| 2 |

A、y=3cos(2x+
| ||
B、y=3cos(2x-
| ||
C、y=3sin(2x+
| ||
D、y=3sin(2x-
|
函数y=f(x)在区间(-2,2)上的图象是连续不断的,且方程f(x)=0在(-2,2)上仅有一个实根x=0,则f(-1)f(1)的值( )
| A、大于0 |
| B、小于0 |
| C、等于0 |
| D、与0的大小关系无法确定 |
已知集合M={(x,y)|x+y<0,xy>0},N={(x,y)|x<0,y<0},那么( )
| A、N?M | B、M?N |
| C、M=N | D、M?N |