题目内容
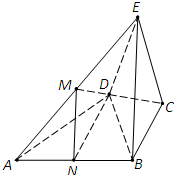如图，在四棱锥E-ABCD中，△ABD为正三角形，EB=ED，CB=CD．（1）求证：EC⊥BD；
（2）若AB⊥BC，M，N分别为线段AE，AB的中点，求证：平面DMN∥平面BEC．
考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：（1）取BD的中点O，连接OE，OC，证明BD⊥平面EOC，即可证明EC⊥BD；
（2）证明DN∥平面BEC；MN∥平面BEC，利用面面平行的判定定理，即可得证．
（2）证明DN∥平面BEC；MN∥平面BEC，利用面面平行的判定定理，即可得证．
解答：
证明：（1）取BD的中点O，连接OE，OC，则
∵EB=ED，CB=CD，
∴BD⊥EO，BD⊥CO，
∵EO∩CO=O，
∴BD⊥平面EOC，
∵EC?平面EOC，
∴EC⊥BD；
（2）∵△ABD为正三角形，N为AB的中点，
∴DN⊥AB，
∴AB⊥BC，
∴DN∥BC，
∵DN?平面BEC，BC?平面BEC，
∴DN∥平面BEC；
∵M，N分别为线段AE，AB的中点，
∴MN∥BE，
∵MN?平面BEC，BE?平面BEC，
∴MN∥平面BEC；
∵DN∩MN=N，
∴平面DMN∥平面BEC．
证明：（1）取BD的中点O，连接OE，OC，则∵EB=ED，CB=CD，
∴BD⊥EO，BD⊥CO，
∵EO∩CO=O，
∴BD⊥平面EOC，
∵EC?平面EOC，
∴EC⊥BD；
（2）∵△ABD为正三角形，N为AB的中点，
∴DN⊥AB，
∴AB⊥BC，
∴DN∥BC，
∵DN?平面BEC，BC?平面BEC，
∴DN∥平面BEC；
∵M，N分别为线段AE，AB的中点，
∴MN∥BE，
∵MN?平面BEC，BE?平面BEC，
∴MN∥平面BEC；
∵DN∩MN=N，
∴平面DMN∥平面BEC．
点评：本题主要考查平面图形中的线线关系，线面平行和线面垂直的判定宝理．熟练掌握线面、面面平行与垂直的判定定理和性质定理是解题的关键．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
如图，母线长为2的圆锥PO中，已知AB是半径为1的⊙O的直径，点C在AB弧上，D为AC的中点．