题目内容
已知函数f(x)=(x2-mx+m)•ex(m∈R).
(Ⅰ)若函数f(x)存在零点,求实数m的取值范围;
(Ⅱ)当m<0时,求函数f(x)的单调区间.
(Ⅰ)若函数f(x)存在零点,求实数m的取值范围;
(Ⅱ)当m<0时,求函数f(x)的单调区间.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(Ⅰ)根据函数零点的存在的条件,求实数m的取值范围;
(Ⅱ)当m<0时,求函数的导数,即可求函数f(x)的单调区间.
(Ⅱ)当m<0时,求函数的导数,即可求函数f(x)的单调区间.
解答:
解:(Ⅰ)若函数f(x)存在零点,即f(x)=(x2-mx+m)•ex=0有解,
则等价为x2-mx+m=0有解,即△=m2-4m≥0,
解得m≥4或m≤0,
即实数m的取值范围m≥4或m≤0;
(Ⅱ)当m<0时,函数的导数f′(x)=[x2+(2-m)x]ex=x[x-(m-2)]•ex,
∵m<0,
∴由f′(x)>0,得x>0或x<m-2;
由f′(x)<0,得m-2<x<0;
故f(x)的递增区间为(0,+∞)和(-∞,m-2),f(x)的递减区间为(m-2,0).
则等价为x2-mx+m=0有解,即△=m2-4m≥0,
解得m≥4或m≤0,
即实数m的取值范围m≥4或m≤0;
(Ⅱ)当m<0时,函数的导数f′(x)=[x2+(2-m)x]ex=x[x-(m-2)]•ex,
∵m<0,
∴由f′(x)>0,得x>0或x<m-2;
由f′(x)<0,得m-2<x<0;
故f(x)的递增区间为(0,+∞)和(-∞,m-2),f(x)的递减区间为(m-2,0).
点评:本题主要考查函数零点的应用以及函数单调性和导数之间的关系,考查学生的运算能力.

练习册系列答案
相关题目
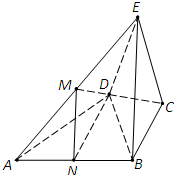 如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.
如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD. 已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.
已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.