题目内容
在△ABC中,a=1,b=
,c=
(x>0,e=2.71828…)).
(1)求△ABC的最大角;
(2)试比较am+bm与cm(m∈R)的大小.
| ex-e-x |
| 2 |
| ex+e-x |
| 2 |
(1)求△ABC的最大角;
(2)试比较am+bm与cm(m∈R)的大小.
考点:余弦定理
专题:三角函数的求值
分析:(1)利用基本不等式求出c的最小值,利用作差法比较b与c的大小,判断出C为最大值,根据余弦定理表示出cosC,即可确定出C的度数;
(2)由C为直角,利用勾股定理列出关系式,利用锐角三角函数定义表示出a与b,进而表示出am+bm,分m<2;m=2;m>2三种情况比较am+bm与cm(m∈R)的大小即可.
(2)由C为直角,利用勾股定理列出关系式,利用锐角三角函数定义表示出a与b,进而表示出am+bm,分m<2;m=2;m>2三种情况比较am+bm与cm(m∈R)的大小即可.
解答:
解:(1)∵c=
≥
=1=a,
b-c=-ex<0,即b<c.
∴c所对的角C是△ABC的最大角,
∵cosC=
=0,
∴C=90°;
(2)∵C=90°,
∴a2+b2=c2,
∴a=c•sinA,b=c•cosA,
∴am+bm=cm(sinmA+cosmA),
分三种情况考虑:
①当m<2时,am+bm>cm(sin2A+cos2A)=cm;
②当m=2时,am+bm=cm;
②当m>2时,sinmA+cosmA<sin2A+cos2A=1,此时am+bm<cm(sin2A+cos2A)=cm.
| ex+e-x |
| 2 |
2
| ||
| 2 |
b-c=-ex<0,即b<c.
∴c所对的角C是△ABC的最大角,
∵cosC=
12+(
| ||||
| ex-e-x |
∴C=90°;
(2)∵C=90°,
∴a2+b2=c2,
∴a=c•sinA,b=c•cosA,
∴am+bm=cm(sinmA+cosmA),
分三种情况考虑:
①当m<2时,am+bm>cm(sin2A+cos2A)=cm;
②当m=2时,am+bm=cm;
②当m>2时,sinmA+cosmA<sin2A+cos2A=1,此时am+bm<cm(sin2A+cos2A)=cm.
点评:此题考查了余弦定理,以及基本不等式的运用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
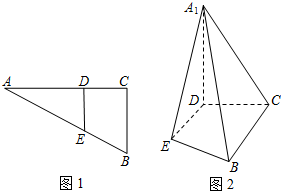 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)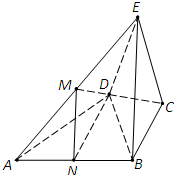 如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.
如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD. 已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.
已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.