题目内容
已知f（x）=|x+20|-|16-x|．（x∈R）．
（1）解不等式f（x）≥0；
（2）若关于x的不等式f（x）≥m的解集是非空集合，求实数m的取值范围．
（1）解不等式f（x）≥0；
（2）若关于x的不等式f（x）≥m的解集是非空集合，求实数m的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（1）不等式即|x+20|-|16-x|≥0，即 （x+20）2≥（x-16）2，由此求得不等式的解集．
（2）由题意可得 m≤fmax（x），根据绝对值三角不等式求得f（x）的最大值为36，从而求得m的范围．
（2）由题意可得 m≤fmax（x），根据绝对值三角不等式求得f（x）的最大值为36，从而求得m的范围．
解答：
解：（1）不等式即|x+20|-|16-x|≥0，即 （x+20）2≥（x-16）2，
求得x≥-2，故不等式的解集为[-2，+∞）．
（2）∵关于x的不等式f（x）≥m的解集是非空集合，∴m≤fmax（x），
根据f（x）=|x+20|-|16-x|≤|x+20-（x-16）|=36，
∴fmax（x）=36，∴m≤36．
求得x≥-2，故不等式的解集为[-2，+∞）．
（2）∵关于x的不等式f（x）≥m的解集是非空集合，∴m≤fmax（x），
根据f（x）=|x+20|-|16-x|≤|x+20-（x-16）|=36，
∴fmax（x）=36，∴m≤36．
点评：本题主要考查绝对值不等式的解法，绝对值三角不等式，体现了转化的数学思想，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
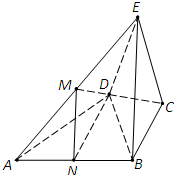如图，在四棱锥E-ABCD中，△ABD为正三角形，EB=ED，CB=CD．
已知平行四边形ABCD的对角线相交于点O，G是平行四边形ABCD所在平面外一点，且GA=GC，GB=GD，求证：GO⊥平面ABCD．