题目内容
 如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点.
如图,母线长为2的圆锥PO中,已知AB是半径为1的⊙O的直径,点C在AB弧上,D为AC的中点.(1)求圆锥PO的表面积;
(2)证明:平面ACP⊥平面POD.
考点:平面与平面垂直的判定,旋转体(圆柱、圆锥、圆台)
专题:综合题,空间位置关系与距离
分析:(1)圆锥PO的表面积为S侧+S底;
(2)利用OA=OC,D为AC的中点,证明AC⊥OD,利用PO⊥底面⊙O,AC?底面⊙O,证明PO⊥AC,从而AC⊥平面POD,即可证明平面ACP⊥平面POD.
(2)利用OA=OC,D为AC的中点,证明AC⊥OD,利用PO⊥底面⊙O,AC?底面⊙O,证明PO⊥AC,从而AC⊥平面POD,即可证明平面ACP⊥平面POD.
解答:
 (1)解:由已知圆锥PO的表面积为S侧+S底=2π+π=3π;
(1)解:由已知圆锥PO的表面积为S侧+S底=2π+π=3π;
(2)证明:连接OC,在△AOC中,
因为OA=OC,D为AC的中点,
所以AC⊥OD,
又PO⊥底面⊙O,AC?底面⊙O,
所以PO⊥AC
因为DO、PO是平面POD内的两条相交直线,
所以AC⊥平面POD,
又因为AC?平面ACP,
所以平面ACP⊥平面POD.
 (1)解:由已知圆锥PO的表面积为S侧+S底=2π+π=3π;
(1)解:由已知圆锥PO的表面积为S侧+S底=2π+π=3π;(2)证明:连接OC,在△AOC中,
因为OA=OC,D为AC的中点,
所以AC⊥OD,
又PO⊥底面⊙O,AC?底面⊙O,
所以PO⊥AC
因为DO、PO是平面POD内的两条相交直线,
所以AC⊥平面POD,
又因为AC?平面ACP,
所以平面ACP⊥平面POD.
点评:本题考查圆锥PO的表面积,考查线面、面面垂直,考查学生分析解决问题的能力,正确运用线面、面面垂直的判定定理是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
给定数列,1,2+3+4,5+6+7+8+9,10+11+12+13+14+15+16,…则这个数列的通项公式是( )
| A、an=2n2+3n-1 |
| B、an=n2+5n-5 |
| C、an=2n3-3n2+3n-1 |
| D、an=2n3-n2+n-2 |
设f(x)=x2-2x-4lnx,则f(x)的增区间为( )
| A、(0,+∞) |
| B、(2,+∞) |
| C、(-∞,-1) |
| D、(∞,-1)和(2,+∞) |
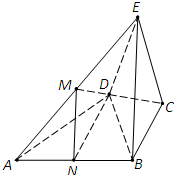 如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.
如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.