题目内容
抛物线y2=4x上一点P到直线x=-1的距离与到点Q（2，2）的距离之差的最大值为（ ）
| A、3 | ||
B、
| ||
| C、5 | ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：当P，Q，F共线时，P到直线x=-1的距离与到点Q（2，2）的距离之差取最大值，由此能求出结果．
解答：
解：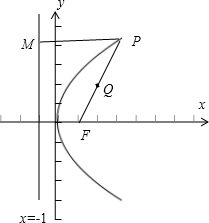
如图，由抛物线的定义知：
抛物线y2=4x上一点P到直线x=-1的距离|PM|=|PF|，
∴当P，Q，F共线时，
P到直线x=-1的距离与到点Q（2，2）的距离之差取最大值，
∵F（1，0），Q（2，2），
∴[|PM|-|PQ|]max
=[|PF|-|PQ|]max
=|QF|
=
=
，
故选：D．
如图，由抛物线的定义知：抛物线y2=4x上一点P到直线x=-1的距离|PM|=|PF|，
∴当P，Q，F共线时，
P到直线x=-1的距离与到点Q（2，2）的距离之差取最大值，
∵F（1，0），Q（2，2），
∴[|PM|-|PQ|]max
=[|PF|-|PQ|]max
=|QF|
=
| (2-1)2+22 |
| 5 |
故选：D．
点评：本题考查两线段之差的最大值的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
若向量
=（1，1-x），
=（1，1+x），则函数f（x）=
是（ ）
| a |
| b |
| ||||||
| 4-|x-4| |
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、减函数 |
在△ABC中，三边a，b，c所对的角分别为A，B，C，若a2-b2=
bc，sinC=2
sinB，则角A=（ ）
| 3 |
| 3 |
| A、30° | B、45° |
| C、150° | D、135° |
从2名男生和2名女生中，任意选择两人在星期六、星期日参加某公益活动，每天一人，则星期六安排一名男生、星期日安排一名女生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）的导函数为f′（x），若对任意x∈R都有f′（x）＞f（x）成立，则（ ）
| A、f（ln2014）＜2014f（0） |
| B、f（ln2014）=2014f（0） |
| C、f（ln2014）＞2014f（0） |
| D、f（ln2014）与2014f（0）的大小关系不确定 |