Question

直线4x+3y-12=0与x轴、y轴分别交于A，B两点．
（1）求∠BAO的平分线所在直线的方程；
（2）求点O到∠BAO的平分线的距离；
（3）求过B与∠BAO的平分线垂直的直线方程．

Answer 1

考点：直线的截距式方程,直线的一般式方程与直线的垂直关系

专题：直线与圆

分析：（1）设∠BAO=2α，（α为锐角），可得-tan2α=-

4

3

，利用

2tanα

1-tan2α

=

4

3

，解得tanα，可得∠BAO的平分线所在直线的斜率，再利用点斜式即可得出；
（2）利用点到直线的距离公式即可得出；
（3）由于要求的直线与x+2y-3=0垂直，可得斜率k=2．再利用斜截式即可得出．

解答： 解：由直线4x+3y-12=0化为

x

3

+

y

4

=1或y=-

4

3

x+4．
（1）设∠BAO=2α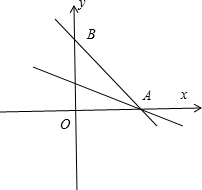，（α为锐角）．
则-tan2α=-

4

3

，即tan2α=

4

3

，
∴

2tanα

1-tan2α

=

4

3

，解得tanα=

1

2

．
∴∠BAO的平分线所在直线的斜率为-

1

2

，其方程为y=-

1

2

(x-3)，化为x+2y-3=0；
（2）点O到∠BAO的平分线的距离d=

3

5

=

3 5

5

；
（3）∵要求的直线与x+2y-3=0垂直，∴斜率k=2．
由斜截式可得y=2x+4．

点评：本题考查了直线方程的各种形式、倍角公式、相互垂直的直线斜率之间的关系，考查了计算能力，属于基础题．