题目内容
设f(x)=asin(πx+α)+bcos(πx+β),其中a、b、α、β为非零常数.若f(2013)=-1,则f(2014)等于( )
| A、-1 | B、0 | C、1 | D、2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由题意和诱导公式可得asinα+bcosβ=1,把x=2014代入由诱导公式化简可得f(2014)=asinα+bcosβ,整体代入计算可得.
解答:
解:∵f(x)=asin(πx+α)+bcos(πx+β),
∴f(2013)=asin(2013π+α)+bcos(2013π+β)=-1,
由诱导公式化简可得:-asinα-bcosβ=-1,即asinα+bcosβ=1
∴f(2014)=asin(2014π+α)+bcos(2014π+β)
=asinα+bcosβ=1,
故选:C.
∴f(2013)=asin(2013π+α)+bcos(2013π+β)=-1,
由诱导公式化简可得:-asinα-bcosβ=-1,即asinα+bcosβ=1
∴f(2014)=asin(2014π+α)+bcos(2014π+β)
=asinα+bcosβ=1,
故选:C.
点评:本题考查诱导公式,整体代入是解决问题的关键,属基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
若复数z满足iz=1+2i,则在复平面内,z的共轭复数
对应的点所在象限是( )
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
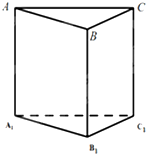 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2| 34 |
A、
| ||||
B、
| ||||
C、360
| ||||
D、
|