题目内容
14. 为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
| 分组 | 频数 | 频率 |
| [0,30) | 3 | 0.03 |
| [30,60) | 3 | 0.03 |
| [60,90) | 37 | 0.37 |
| [90,120) | m | n |
| [120,150) | 15 | 0.15 |
| 合计 | M | N |
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.
分析 (I)由频率分布表利用频率=$\frac{频数}{总数}$,能求出M,m,n,前能出频率分布直方图示.
(Ⅱ)先求出全区90分以上学生的频率,由此能估计这次测试中我市学生成绩在90分以上的人数.
(Ⅲ)利用列举法能求出被选中2人分数均不超过30分的概率.
解答 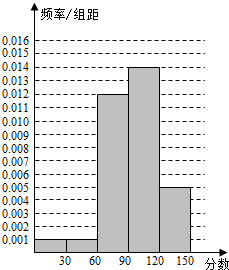 解:(I)由频率分布表得M=$\frac{3}{0.03}$=100,
解:(I)由频率分布表得M=$\frac{3}{0.03}$=100,
∴m=100-(3+3+37+15)=42,
n=$\frac{42}{100}$=0.42,N=0.03+0.03+0.37+0.42+0.15=1,
频率分布表如右图所示.
(Ⅱ)由题意知,全区90分以上学生估计为$\frac{42+15}{100}×18000=10260$(人).
(Ⅲ)设考试成绩在(0,30]内的3 人分别为A、B、C,考试成绩在(30,60]内的3人分别为a,b,c,
从不超过60分的6人中,任意取2人的结果有15个:
(A,B),(A,C),(A,a),(A,b),(A,c),(B,C),(B,a),(B,b),(B,c),(C,a),(C,b),(C,c),(a,b),(a,c),(b,c),
被选中2人分数均不超过30分的情况有:(A,B),(A,C),(B,C),共3个,
∴被选中2人分数均不超过30分的概率p=$\frac{3}{15}=\frac{1}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图和列举法的合理运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
11.已知函数f(x)=(x-a)2+(ex-a)2(a∈R),若存在x0∈R,使得f(x0)≤$\frac{1}{2}$成立,则实数a的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{2}$ |
9.如果f(x)在[-5,5]上是奇函数,且f(3)<f(1),则( )
| A. | f(-1)<f(-3) | B. | f(0)>f(1) | C. | f(-1)<f(1) | D. | f(-3)<f(-5) |
19.已知函数f(x)=lnx+2sinα(α∈(0,$\frac{π}{2}$))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | (0,$\frac{π}{6}$) |
6.化简:$\overrightarrow{AB}$+$\overrightarrow{OA}$-$\overrightarrow{OB}$=( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{BA}$ | C. | 2$\overrightarrow{AB}$ | D. | -2$\overrightarrow{AB}$ |