题目内容
19.已知函数f(x)=lnx+2sinα(α∈(0,$\frac{π}{2}$))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | (0,$\frac{π}{6}$) |
分析 先求出函数的导数,根据f′(x0)=f(x0),可得sin α=$\frac{1}{2}$($\frac{1}{{x}_{0}}$-ln x0),由0<x0<1,可得sin α的范围,即可得出.
解答 解:∵f′(x)=$\frac{1}{x}$,f′(x0)=$\frac{1}{{x}_{0}}$,f′(x0)=f(x0),
∴$\frac{1}{{x}_{0}}$=ln x0+2sinα,
∴sinα=$\frac{1}{{2x}_{0}}$-$\frac{1}{2}$ln x0,
又∵0<x0<1,
∴可得 $\frac{1}{2}$($\frac{1}{{x}_{0}}$-ln x0)>$\frac{1}{2}$,即sin α>$\frac{1}{2}$,
∴α∈($\frac{π}{6}$,$\frac{π}{2}$).
故选:C.
点评 本题考查了导数的运算法则、对数函数和正切函数的单调性,属于中档题.

练习册系列答案
相关题目
16.若实数x,y满足$\sqrt{{x}^{2}+(y-13)^{2}}$-$\sqrt{{x}^{2}+(y+13)^{2}}$=10,则动点P(x,y)的轨迹方程是( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x>0) | B. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x<0) | ||
| C. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y>0) | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y<0) |
14. 为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
(2)若我市参加本次考试的学生有18000人,试估计这次测试中我市学生成绩在90分以上的人数;
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.
 为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
| 分组 | 频数 | 频率 |
| [0,30) | 3 | 0.03 |
| [30,60) | 3 | 0.03 |
| [60,90) | 37 | 0.37 |
| [90,120) | m | n |
| [120,150) | 15 | 0.15 |
| 合计 | M | N |
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.
4.某校为了解高一学生的数学水平,随机抽取了高一男,女生各40人参加数学等级考试,得到男生数学成绩的频数分布表和女生数学成绩的频率分布直方图如下:
男生数学成绩的频数分布表
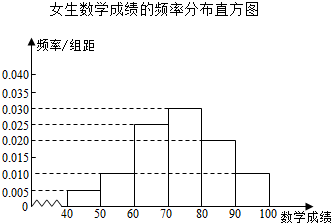
(Ⅰ)画出男生数学成绩的频率分布直方图,并比较该校高一男,女生数学成绩的方差大小;(只需写出结论)
(Ⅱ)根据女生数学成绩的频率分布直方图,估计该校高一女生的数学平均成绩;
(Ⅲ)依据学生的数学成绩,将学生的数学水平划分为三个等级:
估计该校高一男,女生谁的“数学水平良好”的可能性大,并说明理由.
男生数学成绩的频数分布表
| 成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 16 | 10 | 4 |

(Ⅰ)画出男生数学成绩的频率分布直方图,并比较该校高一男,女生数学成绩的方差大小;(只需写出结论)
(Ⅱ)根据女生数学成绩的频率分布直方图,估计该校高一女生的数学平均成绩;
(Ⅲ)依据学生的数学成绩,将学生的数学水平划分为三个等级:
| 数学成绩 | 低于70分 | 70~90分 | 不低于90分 |
| 数学水平 | 一般 | 良好 | 优秀 |
8.函数f(x)=cos2(x-$\frac{π}{4}$)-cos2(x+$\frac{π}{4}$)的最大值和最小正周期分别为( )
| A. | $\frac{1}{2}$,π | B. | 1,π | C. | $\frac{1}{2}$,$\frac{π}{2}$ | D. | 1,$\frac{π}{2}$ |
9.点P(-2,1)关于直线l:x-y+1=0对称的点P′的坐标是( )
| A. | (1,0) | B. | (0,1) | C. | (0,-1) | D. | (-1,0) |
 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,