题目内容
已知等差数列{an}的公差大于0,其中a3,a5是方程x2-14x+45=0的两根,数列{bn}的前n项和为Sn,且Sn=
(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn,数列{cn}的前n项和为Tn,求证:Tn≥
.
| 1-bn |
| 2 |
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn,数列{cn}的前n项和为Tn,求证:Tn≥
| 1 |
| 3 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由二次方程可求得a3,a5,由等差数列的通项公式可求得an,由bn=Sn-Sn-1可得数列递推式,可判断{bn}为等比数列,从而可求;
(Ⅱ)利用错位相减法可求得Tn,通过作差可判断{Tn}为递增数列,从而可得Tn≥T1,得到结论;
(Ⅱ)利用错位相减法可求得Tn,通过作差可判断{Tn}为递增数列,从而可得Tn≥T1,得到结论;
解答:
解:(Ⅰ)∵a3,a5是方程x2-14x+45=0的两根,且数列{an}的公差d>0,
解得a3=5,a5=9,则公差d=
=2.
∴an=a5+(n-5)d=2n-1.
当n=1时,有b1=S1=1-
b1,∴b1=
,
当n≥2时,有bn=Sn-Sn-1=
(bn-1-bn),
∴3bn=bn-1,
∵b1=
≠0,∴
=
(n≥2).
∴数列{bn}是以
为首项,以
为公比的等比数列,
∴bn=b1•qn-1=
;
(Ⅱ)由(Ⅰ)知cn=an•bn=
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
+
,②
①-②得
Tn=
+
+
+…+
-
=
+2(
+
+…+
)-
=
+2×
-
=
-
,
∴Tn=1-
,
∵Tn+1-Tn=-
+
=
>0,
∴{Tn}为递增数列,
∴Tn≥T1=
.
解得a3=5,a5=9,则公差d=
| a5-a3 |
| 5-3 |
∴an=a5+(n-5)d=2n-1.
当n=1时,有b1=S1=1-
| 1 |
| 2 |
| 2 |
| 3 |
当n≥2时,有bn=Sn-Sn-1=
| 1 |
| 2 |
∴3bn=bn-1,
∵b1=
| 2 |
| 3 |
| bn |
| bn-1 |
| 1 |
| 3 |
∴数列{bn}是以
| 2 |
| 3 |
| 1 |
| 3 |
∴bn=b1•qn-1=
| 1 |
| 3n |
(Ⅱ)由(Ⅰ)知cn=an•bn=
| 2n-1 |
| 3n |
∴Tn=
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 3 |
| 33 |
| 5 |
| 34 |
| 2n-3 |
| 3n |
| 2n-1 |
| 3n+1 |
①-②得
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 2n-1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 2n-1 |
| 3n+1 |
=
| 1 |
| 3 |
| ||||
1-
|
| 2n-1 |
| 3n+1 |
| 2 |
| 3 |
| 2n+2 |
| 3n+1 |
∴Tn=1-
| n+1 |
| 3n |
∵Tn+1-Tn=-
| n+2 |
| 3n+1 |
| n+1 |
| 3n |
| 2n+1 |
| 3n+1 |
∴{Tn}为递增数列,
∴Tn≥T1=
| 1 |
| 3 |
点评:本题考查等差数列、等比数列的通项公式及数列求和,考查方程思想,考查学生的运算求解能力,错位相减法对数列求和是高考考查的重点内容,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
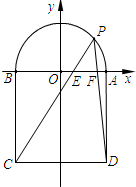 如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.
如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.