题目内容
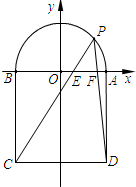 如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.
如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.考点:等比关系的确定
专题:等差数列与等比数列
分析:根据条件先BE,EF,FA,然后利用等比数列的定义,进行证明即可.
解答:
证明:设P(cosα,sinα),C(-1,-2),D(1,-2),
E(x1,0),F(x2,0).
∵点P、E、C三点共线,
∴
=
,
∴x1=
-1.
由点P、F、D三点共线,
∴
=
,
∴x2=
+1.
∴BE=x1+1=
,EF=x2-x1=
,FA=
.
∴BE•FA=
×
=
=EF2.
即BE,EF,FA成等比数列.
E(x1,0),F(x2,0).
∵点P、E、C三点共线,
∴
| sinα+2 |
| cosα+1 |
| 2 |
| x1+1 |
∴x1=
| 2(cosα+1) |
| sinα+2 |
由点P、F、D三点共线,
∴
| sinα+2 |
| cosα-1 |
| 2 |
| x2-1 |
∴x2=
| 2(cosα-1) |
| sinα+2 |
∴BE=x1+1=
| 2(cosα+1) |
| sinα+2 |
| 2sinα |
| sinα+2 |
| 2(cosα-1) |
| sinα+2 |
∴BE•FA=
| 2(cosα+1) |
| sinα+2 |
| 2(cosα-1) |
| sinα+2 |
| 4sin2α |
| (sinα+2)2 |
即BE,EF,FA成等比数列.
点评:本题主要考查等比数列的判断,利用条件建立先BE,EF,FA的关系是解决本题的关键,综合性较强,涉及的知识点较大,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知三条直线a,b,c,若a和b是异面直线,b和c是异面直线,那么直线a和c的位置关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行、相交或异面 |
已知函数f(x)=
的图象关于y=x对称,则a=( )
| ax-1 |
| x+2 |
| A、-4 | B、-2 | C、2 | D、4 |
已知x,y∈R+,且x+y=3,则
+
的最小值为( )
| 1 |
| x |
| 1 |
| y |
| A、4 | ||
B、
| ||
C、
| ||
D、
|