题目内容
已知函数f（x）=x+
，x∈（1，+∞）．
（Ⅰ）证明f（x）在区间（1，+∞）是单调增函数；
（Ⅱ）判断f（m）与f（m+1）的大小，其中m＞1．
| 1 |
| x |
（Ⅰ）证明f（x）在区间（1，+∞）是单调增函数；
（Ⅱ）判断f（m）与f（m+1）的大小，其中m＞1．
考点：函数单调性的判断与证明,分段函数的应用
专题：函数的性质及应用
分析：（Ⅰ）用函数单调性的定义证明f（x）在区间[1，+∞）上是增函数；
（Ⅱ）借助增函数来进行判断．
（Ⅱ）借助增函数来进行判断．
解答：
解：（Ⅰ）任取x1，x2∈（1，+∞），且1≤x1＜x2，则f（x2）-f（x1）=（x2+
）-（x1+
）=（x2-x1）+
=
；
∵x2-x1＞0，x1x2＞1，∴x1x2-1＞0，∴f（x2）-f（x1）＞0，即f（x2）＞f（x1），
∴函数在区间（1，+∞）上是增函数；
（Ⅱ）由（Ⅰ）知，函数在区间（1，+∞）上是增函数，
又m＞1，m+1＞m＞1，
∴f（m）＜f（m+1）．
| 1 |
| x2 |
| 1 |
| x1 |
| x1-x2 |
| x1x2 |
| (x2-x1)(x1x2-1) |
| x1x2 |
∵x2-x1＞0，x1x2＞1，∴x1x2-1＞0，∴f（x2）-f（x1）＞0，即f（x2）＞f（x1），
∴函数在区间（1，+∞）上是增函数；
（Ⅱ）由（Ⅰ）知，函数在区间（1，+∞）上是增函数，
又m＞1，m+1＞m＞1，
∴f（m）＜f（m+1）．
点评：本题主要考查函数的单调性的定义以及应用，属于基础题．
练习册系列答案
相关题目
已知命题p：对任意x∈R，总有lg（x2+1）≥0，q：“x＞1”是“x＞2”的充分不必要条件，则下列命题为真命题的是（ ）
| A、p∧q |
| B、（￢p）∧（￢q） |
| C、（￢p）∧q |
| D、p∧（￢q） |
在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．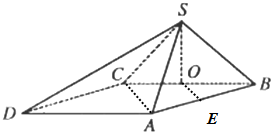
四棱锥S-ABCD中，底面ABCD为平行四边形，且AC⊥AB，O，E分别为BC，AB的中点．已知∠ABC=45°，AB=2，BC=2