题目内容
函数f（x）=Asin（ωx+ϕ）（ω＞0，-
＜ϕ＜
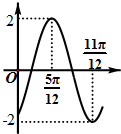
）的部分图象如图所示，则f（x）= ．
| π |
| 2 |
| π |
| 2 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由函数的图象的顶点坐标求出A，由周期求出ω，由图象经过特殊点求得φ的值，可得函数的解析式．
解答：
解：由函数的图象可得A=2，
=
=
-
，∴ω=2．
再根据图象经过点（
，2）可得2sin（2×
+φ）=2，结合，-
＜ϕ＜
，可得φ=-
，
故有f（x）=2sin(2x-
)，
故答案为：2sin（2x-
）．
| T |
| 2 |
| π |
| ω |
| 11π |
| 12 |
| 5π |
| 12 |
再根据图象经过点（
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
故有f（x）=2sin(2x-
| π |
| 3 |
故答案为：2sin（2x-
| π |
| 3 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由图象经过特殊点求出φ的值，属于基础题．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
y=|x2-2x-3|与y=k有4个不同的交点，则k的范围（ ）
| A、（-4，0） |
| B、[0，4] |
| C、[0，4） |
| D、（0，4） |
设数列{an}的前n项和为Sn，点（n，
）（n∈N*）均在函数y=
x+
的图象上，则a2014=（ ）
| Sn |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2014 | B、2013 |
| C、1012 | D、1011 |
设函数f（x）=|x2-4x-5|．若a=30.5，b=ln2，c=logπsin
，则（ ）
| π |
| 12 |
| A、b＞a＞c |
| B、a＞b＞c |
| C、c＞a＞b |
| D、b＞c＞a |