Question

在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．
（Ⅰ）证明AB⊥平面VAD．
（Ⅱ）求面VAD与面VDB所成的二面角余弦值大小
（Ⅲ）若M是AB的中点，在线段VC上是否在一点N，使MN∥平面VAD．若存在，求出M点的位置；若不存在，说明理由．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）作AD的中点O，建立空间直角坐标系，并设正方形边长为1，由量法能证明AB⊥平面VAD．
（Ⅱ）分别求出面VAD的法向量和面VDB的法向量，由此能求出面VAD与面VDB所成的二面角的大小．
（Ⅲ）设VN=λVC，利用向量法能求出MN∥平面VAD，N为VC中点．

解答： （Ⅰ）证明：作AD的中点O，则VO⊥底面ABCD，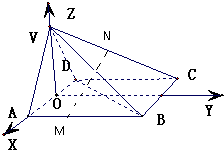
建立如图空间直角坐标系，并设正方形边长为1，
则A（

1

2

，0，0），B（

1

2

，1，0），C（-

1

2

，1，0），
D（-

1

2

，0，0），V（0，0，

3

2

），
∴

AB

=（0，1，0），

AD

=（1，0，0），

AV

=（-

1

2

，0，

3

2

），
由

AB

•

AD

=0，得

AB

⊥

AD

，
由

AB

•

AV

=0，得

AB

⊥

AV

，
又AB∩AV=A，∴AB⊥平面VAD．
（Ⅱ）解：由（Ⅰ）得

AB

=（0，1，0）是面VAD的法向量，
设

n

=（1，y，z）是面VDB的法向量，
则

n • VB =- 1 2 +y- 3 2 z=0 n • BD =-1-y=0

，解得

n

=（1，-1，

3

3

），
∴cos＜

AB

，

n

＞=-

21

7

，
又由题意知，面VAD与面VDB所成的二面角为锐二面角，
∴其大小为arccos

21

7

．
（Ⅲ）解：设VN=λVC，则N（λ，2λ，

3(1-λ)

），M（1，1，0），
设

MN

=x

AD1

+y

AN

，

AD

=（-1，0，0），

AN

=（-

1

2

，0，

3

2

），

-x- 1 2 y=-λ-1 0=2λ-1 3 3 y= 3 (λ-1)

，
∴λ=

1

2

，x=

1

2

，y=-

1

4

，
∴

MN

=

1

2

AD

-

1

4

AM

，
又MN不包含于平面VAD，∴MN∥平面VAD，
此时λ=

1

2

，∴N为VC中点．

点评：本题考查直线与平面垂直的证明，考查二面角的大小的求法，考查直线与平面平行的点的位置的判断与求法，解题时要注意向量法的合理运用．