题目内容
2.函数f(x)=$\sqrt{-{x}^{2}+1}$的定义域是[-1,1].分析 由根式内部的代数式大于等于0,求解一元二次不等式得答案.
解答 解:由-x2+1≥0,解得:-1≤x≤1.
∴函数f(x)=$\sqrt{-{x}^{2}+1}$的定义域是:[-1,1].
故答案为:[-1,1].
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.已知二次函数f(x)=ax2+bx+c,若f(0)=f(6)<f(7),则f(x)在( )
| A. | (-∞,0)上是增函数 | B. | (0,+∞)上是增函数 | C. | (-∞,3)上是增函数 | D. | (3,+∞)上是增函数 |
10.程序框图如图所示,其输出的结果为( )

| A. | 2100-1 | B. | 299-1 | C. | 2100 | D. | 299 |
7.等差数列{an}中Sn是其前n项和,a1=-2010,$\frac{{{S_{2011}}}}{2011}$-$\frac{{{S_{2009}}}}{2009}$=2,则S2010的值为( )
| A. | -2009 | B. | 2009 | C. | -2010 | D. | 2010 |
14.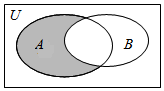 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|x≤1} | D. | {x|1≤x<2} |