题目内容
7.等差数列{an}中Sn是其前n项和,a1=-2010,$\frac{{{S_{2011}}}}{2011}$-$\frac{{{S_{2009}}}}{2009}$=2,则S2010的值为( )| A. | -2009 | B. | 2009 | C. | -2010 | D. | 2010 |
分析 Sn=$n{a}_{1}+\frac{n(n-1)d}{2}$,可得$\frac{{S}_{n}}{n}$=$\frac{d}{2}n$+$({a}_{1}-\frac{d}{2})$为等差数列,公差为$\frac{d}{2}$.即可得出.
解答 解:∵Sn=$n{a}_{1}+\frac{n(n-1)d}{2}$,∴$\frac{{S}_{n}}{n}$=$\frac{d}{2}n$+$({a}_{1}-\frac{d}{2})$为等差数列,公差为$\frac{d}{2}$.
∴$\frac{{{S_{2011}}}}{2011}$-$\frac{{{S_{2009}}}}{2009}$=2=2×$\frac{d}{2}$,解得$\frac{d}{2}$=1.
∴$\frac{{S}_{2010}}{2010}$=$\frac{{a}_{1}}{1}$+2009×$\frac{d}{2}$=-2010+2009=-1.
S2010=-2010,
故选:C.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.将直线l沿y轴的负方向平移a(a>0)个单位,再沿x轴正方向平移a+1个单位得直线l',此时直线l'与l重合,则直线l'的斜率为( )
| A. | $\frac{a}{a+1}$ | B. | -$\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | -$\frac{a+1}{a}$ |
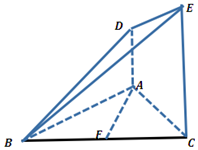 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,