题目内容
11.已知圆O和圆C的极坐标方程分别为ρ=2和ρ=4sinθ,点P为圆O上任意一点.(1)若射线OP交圆C于点Q,且其方程为θ=$\frac{π}{3}$,求|PQ|得长;
(2)已知D(2,$\frac{3}{2}$π),若圆O和圆C的交点为A,B,求证:|PA|2+|PB|2+|PD|2为定值.
分析 (1)θ=$\frac{π}{3}$代入ρ=4sinθ,可得ρ=2$\sqrt{3}$,即可求出|PQ|;
(2)求出A,B,D的直角坐标,利用两点间的距离公式,即可得出结论.
解答 (1)解:θ=$\frac{π}{3}$代入ρ=4sinθ,可得ρ=2$\sqrt{3}$,
∴|PQ|=2$\sqrt{3}$-2;
(2)证明:由题意,A(-$\sqrt{3}$,1),B($\sqrt{3}$,1),D(0,-2),
设P(x,y),则|PA|2+|PB|2+|PD|2=(x+$\sqrt{3}$)2+(y-1)2+(x-$\sqrt{3}$)2+(y-1)2+x2+(y+2)2=3(x2+y2)+12=24,为定值.
点评 本题考查极坐标方程,考查两点间的距离公式,比较基础.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
19.将直线l沿y轴的负方向平移a(a>0)个单位,再沿x轴正方向平移a+1个单位得直线l',此时直线l'与l重合,则直线l'的斜率为( )
| A. | $\frac{a}{a+1}$ | B. | -$\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | -$\frac{a+1}{a}$ |
3.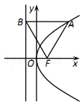 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
20.已知函数f(x)=$\left\{\begin{array}{l}-{(x-1)^2},({x<1})\\(3-a)x+4a,({x≥1})\end{array}$为增函数,则实数a的取值范围是( )
| A. | -1≤a<3 | B. | a<3 | C. | a>3或a≤-1 | D. | -1<a<3 |
1.四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,则该四棱锥的外接球的半径为( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |