题目内容
17.已知命题p:?x∈R,使(m+1)(x2+1)≤0,命题q:?x∈R,x2+mx+1>0.若p∧q为真命题,则实数m的取值范围为-2<m≤-1.分析 若p∧q为真命题,则命题p,q全为真命题,进而可得实数m的取值范围.
解答 解:若p∧q为真命题,则命题p,q全为真命题,
若命题p:?x∈R,使(m+1)(x2+1)≤0,
则m+1≤0,解得:m≤-1,
若命题q:?x∈R,x2+mx+1>0,
则△=m2-4<0,
解得:-2<m<2,
综上可得:-2<m≤-1,
故答案为:-2<m≤-1
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题,特称命题等知识点,难度中档.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
15.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)<1,f(0)=11,则不等式f(x)>$\frac{{e}^{x}+10}{{e}^{x}}$(其中e为自然对数的底数)的解集为( )
| A. | (10,+∞) | B. | (-∞,0)∪(11,+∞) | C. | (-∞,11) | D. | (-∞,0) |
9.设f(x)是偶函数,且在(0,+∞)上是增函数,又f(5)=0,则使f(x)>0的x的取值范围是( )
| A. | -5<x<0或x>5 | B. | x<-5或x>5 | C. | -5<x<5 | D. | x<-5或0<x<5 |
7.图中的阴影表示的集合中是( )


| A. | A∩∁UB | B. | B∩∁UA | C. | ∁U(A∩B) | D. | ∁U(A∪B) |
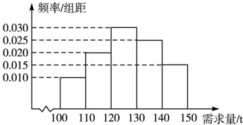 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.