题目内容
设f(x)的定义域为(0,+∞),且在(0,+∞)是递增的,f(
)=f(x)-f(y).
(1)求证:f(1)=0,f(xy)=f(x)+f(y);
(2)设f(2)=1,解不等式f(x)-f(
)≤2.
| x |
| y |
(1)求证:f(1)=0,f(xy)=f(x)+f(y);
(2)设f(2)=1,解不等式f(x)-f(
| 1 |
| x-3 |
考点:抽象函数及其应用,其他不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)令x=y=1得f(1)=0,则有f(xy)=f(
)=f(x)-f(
)=f(x)-[f(1)-f(y)]=f(x)+f(y),(2)由f(
)=f(x)-f(y)=f(x2-3x),然后可求f(4)=2,转化为不等式求解.
| x | ||
|
| 1 |
| y |
| x |
| y |
解答:
解:(1)证明:f(
)=f(x)-f(y),
令x=y=1,则有:f(1)=f(1)-f(1)=0,
f(xy)=f(
)=f(x)-f(
)=f(x)-[f(1)-f(y)]=f(x)+f(y).
(2)∵f(x)-f(
)=f(x)-[f(1)-f(x-3)]=f(x)+f(x-3)=f(x2-3x),
∵2=2×1=2f(2)=f(2)+f(2)=f(4),
∴f(x)-f(
)≤2等价于:f(x2-3x)≤f(4)①,
且x>0,x-3>0(由f(x)定义域为(0,+∞)可得),
∵x(x-3)=x2-3x>0,4>0,
又f(x)在(0,+∞)上为增函数,
∴①?x2-3x≤4⇒-1≤x≤4,又x>3,
∴原不等式的解集为;{x|3<x≤4}.
| x |
| y |
令x=y=1,则有:f(1)=f(1)-f(1)=0,
f(xy)=f(
| x | ||
|
| 1 |
| y |
(2)∵f(x)-f(
| 1 |
| x-3 |
∵2=2×1=2f(2)=f(2)+f(2)=f(4),
∴f(x)-f(
| 1 |
| x-3 |
且x>0,x-3>0(由f(x)定义域为(0,+∞)可得),
∵x(x-3)=x2-3x>0,4>0,
又f(x)在(0,+∞)上为增函数,
∴①?x2-3x≤4⇒-1≤x≤4,又x>3,
∴原不等式的解集为;{x|3<x≤4}.
点评:本题考查抽象函数,抓住解题关键f(
)=f(x)-f(y).利用取特值求解.
| x |
| y |

练习册系列答案
相关题目
如函数f(x)=-x2+2ax与函数g(x)=
在区间(2,5]上都是减函数,则实数a的取值范围为( )
| a |
| x+1 |
| A、(-2,0] |
| B、(-2,0) |
| C、(0,2) |
| D、(0,2] |
已知x,y是正数,且满足2<x+2y<4.那么x2+y2的取值范围是( )
A、(
| ||||
B、(
| ||||
| C、(1,16) | ||||
D、(
|
已知集合A={y|y=2x,x∈R},B={x||x|≤2,x∈Z},则A∩B=( )
| A、(0,2] |
| B、[0,2] |
| C、{1,2} |
| D、{0,1,2} |

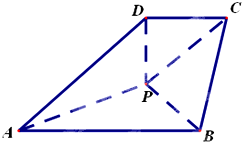 四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.
四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.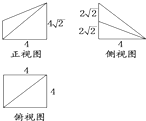 如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为
如图所示是一个几何体的三视图.正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).则该几何体的体积为