Question

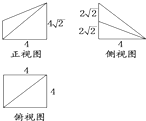如图所示是一个几何体的三视图．正视图、俯视图、侧视图（其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形，尺寸如图所示）．则该几何体的体积为

 

．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知中几何体的三视图．画出几何体的直观图，进而根据棱锥体积公式，可得答案．

解答： 解：由已知中几何体的三视图，可得几何体的直观图如下所示：

该几何体由四棱锥P-ABCD和三棱锥P-BCE组成，
四棱锥P-ABCD的体积为：

1

3

×4×4×4

2

=

64 2

3

，
三棱锥P-BCE的体积为：

1

3

×(

1

2

×4×2

2

)×4=

16 2

3

，
故该几何体的体积为

64 2

3

+

16 2

3

=

80 2

3

；
故答案为：

80 2

3

点评：本题考查的知识点是由三视图求体积，其中根据三视图判断几何体的形状及相关棱长的长度是解答的关键．