题目内容
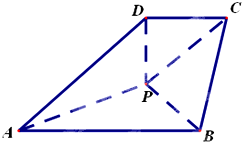 四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.
四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.(Ⅰ)证明:PD⊥面PAB;
(Ⅱ)求二面角P-CB-A的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)证明PD⊥PA,PD⊥PB,利用直线与平面垂直的判定定理证明PD⊥面PAB.
(Ⅱ)取AB中点M,连PM,DM,作PN⊥DM,垂足为N,再作NH⊥BC,连HN.说明∠NHP二面角P-CB-A的平面角.
在△NHP中,求解二面角A-PB-C的平面角的余弦值即可.
(Ⅱ)取AB中点M,连PM,DM,作PN⊥DM,垂足为N,再作NH⊥BC,连HN.说明∠NHP二面角P-CB-A的平面角.
在△NHP中,求解二面角A-PB-C的平面角的余弦值即可.
解答:
 解:(Ⅰ)证明:易知在梯形ABCD中,AD=
解:(Ⅰ)证明:易知在梯形ABCD中,AD=
,而PD=1,AP=2,则PD⊥PA
同理PD⊥PB,故PD⊥面PAB;…(6分)
(Ⅱ)取AB中点M,连PM,DM,
作PN⊥DM,垂足为N,再作NH⊥BC,连HN.
易得AB⊥面DPM,则面ABCD⊥面DPM
于是PN⊥面ABCD,BC⊥面NPH
即∠NHP二面角P-CB-A的平面角.
在△NHP中,PN=
,PH=
,NH=1,∴cos∠NHP=
,
故二面角A-PB-C的平面角的余弦值为
…(14分)
 解:(Ⅰ)证明:易知在梯形ABCD中,AD=
解:(Ⅰ)证明:易知在梯形ABCD中,AD=| 5 |
同理PD⊥PB,故PD⊥面PAB;…(6分)
(Ⅱ)取AB中点M,连PM,DM,
作PN⊥DM,垂足为N,再作NH⊥BC,连HN.
易得AB⊥面DPM,则面ABCD⊥面DPM
于是PN⊥面ABCD,BC⊥面NPH
即∠NHP二面角P-CB-A的平面角.
在△NHP中,PN=
| ||
| 2 |
| ||
| 2 |
2
| ||
| 7 |
故二面角A-PB-C的平面角的余弦值为
2
| ||
| 7 |
点评:本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知焦点在y轴上的椭圆
+
=1的长轴长为8,则m等于( )
| x2 |
| 10 |
| y2 |
| m |
| A、4 | B、8 | C、10 | D、16 |
已知直线y=k(x+1)与抛物线C:y2=4x相交于A、B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、
|
(文做)设
<(
)b<(
)a<1,那么( )
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| A、aa<bb<ba |
| B、aa<bb<a |
| C、ab<ba<aa |
| D、ab<aa<ba |
 据气象中心观察和预测:发生于M第的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为时间t(h)内沙尘暴所经过的路程s(km)
据气象中心观察和预测:发生于M第的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为时间t(h)内沙尘暴所经过的路程s(km)