题目内容
设集合A={x|x2+4x=0},集合B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,则a的取值范围为 .
考点:交集及其运算
专题:集合
分析:求解一元二次方程化简结合A,根据A∩B=B,得B⊆A,然后分B为空集,单元素集合,双元素集合讨论求解a的取值范围.
解答:
解:∵A={x|x2+4x=0}={-4,0},
B={x|x2+2(a+1)x+a2-1=0},
由A∩B=B,得B⊆A,
当△=[2(a+1)]2-4(a2-1)<0,即a<-1时,B=∅,符合题意;
当△=[2(a+1)]2-4(a2-1)≥0,即a≥-1时,
若a=-1,则B={0},符合题意;
当a>-1时,由B⊆A,且A={-4,0},
可知a+1=2,a=1.
∴满足A∩B=B的实数a的取值范围为a=1或a≤-1.
故答案为:a=1或a≤-1.
B={x|x2+2(a+1)x+a2-1=0},
由A∩B=B,得B⊆A,
当△=[2(a+1)]2-4(a2-1)<0,即a<-1时,B=∅,符合题意;
当△=[2(a+1)]2-4(a2-1)≥0,即a≥-1时,
若a=-1,则B={0},符合题意;
当a>-1时,由B⊆A,且A={-4,0},
可知a+1=2,a=1.
∴满足A∩B=B的实数a的取值范围为a=1或a≤-1.
故答案为:a=1或a≤-1.
点评:本题考查了交集及其运算,考查了分类讨论的解题思想方法,是中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若函数f(x+1)的定义域是[-1,1],则函数g(x)=
的定义域是( )
| f(2x) |
| x-1 |
| A、[-1,0] |
| B、[0,1) |
| C、[0,1)∪(1.4] |
| D、(0,1) |
已知偶函数f(x)在[0,+∞)单调递减,A(2,1)的其图象上.那么f(x+1)>1的解集为( )
| A、(-2,2) |
| B、(-3,1) |
| C、[0,2) |
| D、(-1,3) |
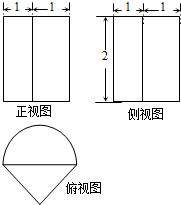 如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )
如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )A、2+3π+4
| ||
B、2+2π+4
| ||
C、8+5π+2
| ||
D、6+3π+2
|
在△ABC中,角A,B,C的对边分别是a,b,c,若∠A:∠B=1:2,a:b=2:3,则cos2A的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
