题目内容
在焦点分别为F1、F2的双曲线上有一点P,若∠F1PF2=
,|PF2|=2|PF1|,则该双曲线的离心率等于( )
| π |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设|PF2|=2|PF1|=2m,利用∠F1PF2=
,推出m、c的关系式.通过双曲线的定义知|PF2|-|PF1|=2a,推出c与a的方程.即可求解离心率.
| π |
| 2 |
解答:
解:不妨设|PF2|=2|PF1|=2m,
则由∠F1PF2=
得|PF2|2+|PF1|2=(2c)2
∴5m2=4c2,m=
c.
又由双曲线的定义知|PF2|-|PF1|=2a,∴m=2a,∵m=
c
∴c=
a.
离心率e=
=
.
故选:D.
则由∠F1PF2=
| π |
| 2 |
∴5m2=4c2,m=
2
| ||
| 5 |
又由双曲线的定义知|PF2|-|PF1|=2a,∴m=2a,∵m=
2
| ||
| 5 |
∴c=
| 5 |
离心率e=
| c |
| a |
| 5 |
故选:D.
点评:本题考查双曲线的基本性质以及双曲线的定义的应用,考查计算能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
“θ≠
”是“cosθ≠
”的( )
| π |
| 3 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若O是A、B、P三点所在直线外一点,且满足条件:
=a1
+a4021
,其中{an}为等差数列,则a2011等于( )
| OP |
| OA |
| OB |
A、-
| ||
| B、1 | ||
C、
| ||
| D、-1 |
已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=( )
| A、2n-1 | ||
B、(
| ||
C、(
| ||
D、
|
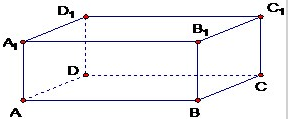 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).